Механизмы внутренних цен

Утверждение 5.2.

Утверждение 5.1.

1) Если некоторый агент в равновесии получает строго меньше ресурса, чем ему необходимо: x_i ^*< r_i, то в равновесии он запросит максимально возможное количество ресурса: s_i ^*= R.

2) Если кто-то из агентов в равновесии просит строго меньше максимума: s_i ^*< R, то это значит, что он получает количество ресурса, оптимальное для него: x_i ^*= r_i, то есть является диктатором.

Введем определение анонимного механизма принятия решений, то есть механизма, симметричного относительно перестановок агентов. Анонимность – демократическое требование, например, в процедурах выборов она отражается в том, что на избирательном участке обмен между двумя избирателями пустыми бланками бюллетеней не меняет результата выборов. То есть все находятся в равных условиях. Тогда при перестановке местами агентов соответственно переставляются и планы этих агентов.

1) Все анонимные механизмы распределения ресурса эквивалентны между собой, то есть приводят при одних и тех же предпочтениях агентов к одним и тем же равновесным количествам ресурса, которые они получают.

2) Так как механизм пропорционального распределения является анонимным (все агенты входят в него симметрично), а все анонимные механизмы эквивалентны между собой, то это значит, что все механизмы распределения ресурсов, которые являются анонимными, эквивалентны механизму пропорционального распределения.

Итак, любая анонимная процедура, удовлетворяющая перечисленным выше трем требованиям, приводит к одним и тем же результатам. А механизм пропорционального распределения (который является анонимным) достаточно прост по своему виду, поэтому прост и для исследования, и для агентов (ресурс делится пропорционально запросам).

Таким образом, утверждение 5.2 говорит, что не нужно выдумывать сложных механизмов распределения ресурса - если ограничиться классом анонимных механизмов, то достаточно рассмотреть механизм пропорционального распределения. Кроме того, оказывается, что механизм пропорционального распределения эквивалентен механизму последовательного распределения, рассчитать равновесие для которого совсем просто.

Механизмы последовательного распределения ресурса заключается в следующем. Это - прямой механизм, т.е. каждого агента спрашивают о том, сколько ресурса ему нужно.

Предположим, что агенты сделали свои сообщения. Упорядочим их по возрастанию сообщений (первый попросил меньше всех ресурса, потом второй и т.д.): 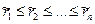. Дальше применяем следующий алгоритм последовательного распределения (положив):

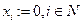Шаг 1. Если мы можем дать каждому агенту столько ресурса, сколько попросил первый агент, то даем всем по 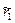(если , то 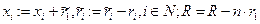). Если не можем, распределяем ресурс между всеми агентами поровну (если 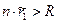, то 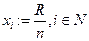)и останавливаем алгоритм.

Шаг 2. Исключаем первого агента из рассмотрения, перенумеровываем агентов и возвращаемся к шагу 1.

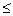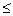Пример 5.2.1. Пусть R=1, r ₁ = 0,3; r ₂=0,4; r ₃=0,5; 0,30,40,5.

Предположим, что все агенты сообщили правду, тогда мы можем дать всем одновременно по минимуму - 0,3: x ₁=0,3; x ₂=0,3; x ₃=0,3.

После первого шага: r ₁ = 0; r₂= 0,1; r ₃=0,2; R= 0,1. Первый агент удовлетворен полностью. Поэтому забываем про него и повторяем для тех, кому ресурс еще необходим. Остаток ресурса, равный 0,1, недостаточен для того, чтобы дать обоим агентам столько, сколько требует первый (бывший второй) – по 0,1, следовательно, мы должны остаток ресурса поделить поровну, т.е. по 0,05. В результате второй агент получит 0,35, третий тоже 0,35:

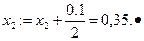
Так работает механизм последовательного распределения. Понятно, что максимум через n шагов, где n – количество агентов, процедура остановится.

Легко показать (сделайте это самостоятельно), что в механизме последовательного распределения ресурса агентам выгодно сообщать достоверную информацию, т.е. сообщение достоверной информации является доминантной стратегией каждого агента.

Другими словами, механизм последовательного распределения является неманипулируемым прямым механизмом.

Рассмотрим на примере 5.2, может ли кто-то из агентов, сообщая неправду, улучшить свое положение?

Первый агент получает оптимальное количество ресурса, ему нет нужды искажать информацию. Предположим, что начинает изменять свое сообщение второй агент (завышает заявку или занижает). Если он будет уменьшать свою заявку, все изменится в тот момент, когда разность от сообщения окажется такой, чтобы, выдавая столько, сколько просит второй агент, нам хватало бы ресурса. Такая разность равна 0,05 (деление поровну). Это значит, что второй агент должен заявить 0,35. Если он заявляет 0,35, то он получает 0,35, что и получал до этого, т.е. никакой выгоды занижение ему не принесло. Если же он сообщит меньше, чем 0,35, то он и получит столько, сколько сообщит, т.е. меньше 0,35. Ему это не выгодно, т.к. в действительности ему требуется 0,4. Таким образом, уменьшать заявку ему не выгодно.

Если же он начинает просить больше, чем 0,4, то вообще ничего не изменится, т.к. на втором шаге ресурса и так не хватает, и его остаток делится поровну между вторым и третьим агентами.

Аналогично для других агентов показывается, что, увеличивая или уменьшая до определенного уровня заявку, они ничего для себя не меняют, а дальнейшее уменьшение заявки дает уменьшение количества получаемого ими ресурса.

Механизмы обратных приоритетов. Механизмы обратных приоритетов, в которых 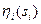является убывающей функцией 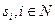, обладают рядом преимуществ по сравнению с механизмами прямых приоритетов. Проведем анализ механизма обратных приоритетов с функциями приоритета

,

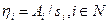где 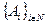- некоторые константы (отметим, что механизм обратных приоритетов не удовлетворяет условию монотонности). Величина A_і характеризует потери ОС, если i -й агент вообще не получит ресурса. Тогда отношение A_i/s_i определяет удельный эффект от использования ресурса. Поэтому механизмы обратных приоритетов иногда называют механизмами распределения ресурса пропорционально эффективности (ПЭ-механизмами).

Пример 5.2.2. Пусть имеются три агента (n= 3), А₁=16, А₂= 9, А₃= 4; R= 18. Предположим сначала, что целью агентов является получение максимального количества ресурса. Определим ситуацию равновесия Нэша. Легко заметить, что функция 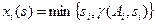достигает максимума по s_i в точке, удовлетворяющей условию . Следовательно, .

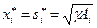Определим параметр 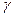из балансового ограничения 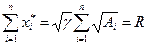. Тогда .

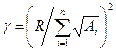Для рассматриваемого примера 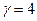, а равновесные заявки, оп­ределяемые из условия 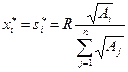, равны: s ₁ *= 8; s ₂ *= 6, s ₃ ^*= 4.

Проверим, что это действительно равновесие Нэша. Возьмем первого агента. Если он уменьшит свою заявку: s ₁ = 7< s₁^*, то s ₁ + s ₂^* + s ₃^*< R. Следовательно, x ₁ =s₁= 7< x ₁ ^*. Если же s₁=9>s₁^*, то .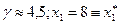

Легко показать, что вычисленные стратегии являются для агентов гарантирующими, то есть максимизируют их выигрыши при наихудших стратегиях остальных.

Если функции предпочтения агентов имеют максимумы в точках 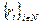и если s_i^* > r_i, то i -й агент закажет ровно r_i и столько же получит, так как при уменьшении заявки его приоритет возрастает.

Именно таким образом выделяется множество приоритетных потребителей ресурса. •

Более того, можно показать, что при достаточно большом числе агентов механизм обратных приоритетов со штрафами за несовпадение ожидаемого и планируемого эффектов оптимален в смысле суммарной эффективности.

Рассмотрим организационную систему, состоящую из центра и п агентов. Целевая функция i -го агента представляет собой разность между вознаграждением, выплачиваемым i -му агенту, и квадратичными затратами, которые зависят от действия агента:

.

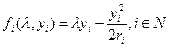Рассмотрим следующую задачу: предположим, что центр хочет, чтобы агенты выбрали действия, сумма которых равна заданной величине R, то есть должно выполняться следующее условие:

.

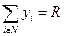Например, центр хочет добиться выполнения подразделениями корпорации суммарного заказа R. Считается, что подразделения выпускают однородную продукцию, и в сумме надо добиться некоторого выпуска (данная задача в качестве примера рассматривалась в разделе 3.1, в настоящем разделе она описывается в рамках общей концепции исследования манипулируемости механизмов планирования). Это - первое ограничение.

Кроме того, центр хочет, чтобы заказ был выполнен с минимальными затратами (см. пример в разделе 3.1). То есть сумма затрат агентов должна быть минимальна: .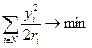

Но, центр имеет возможность управлять только путем выбора функции стимулирования, то есть зависимости вознаграждения агента от результатов его деятельности. Этот параметр 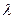, который называется внутрифирменной ценой, один и тот же для всех агентов. Агенты, зная этот параметр, будут выбирать действия, которые максимизируют их целевые функции. Агенты в данном случае независимы друг от друга, так как их целевые функции зависят только от их индивидуальных действий, поэтому задачей центра является выбор внутрифирменной цены таким образом, чтобы затраты агентов были минимальны, было выполнено суммарное действие, и агенты выбирали действия, исходя из максимизации своих целевых функций.

Опишем поведение агента, вычислив точку максимума его целевой функции. Целевая функция агента вогнутая, имеет единственный максимум. Продифференцировав, найдем зависимость действия, выбираемого агентом, от параметра 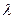: 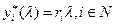. Получаем следующую задачу:

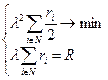
Обозначим 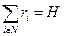. В этой задаче не остается никаких свободных переменных, так как ограничение однозначно определит 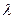, а значение 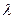, определенное из ограничения, даст значение целевой функции: а именно, 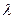должно быть равно отношению 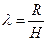. Оптимальным значением целевой функции является величина 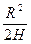. То есть центр имеет полную централизацию, агентам назначаются планы, и агентам выгодно их выполнять. Остается только понять, какие планы назначать агентам, чтобы достичь минимума затрат агентов при выполнении программы суммарного выпуска. Решая эту задачу, получим следующее.

Запишем лагранжиан (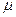– множитель Лагранжа):

.

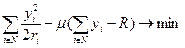Тогда: .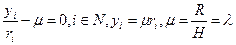

Следовательно, 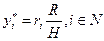, то есть оптимальное действие агента пропорционально его типу.

Таким образом, сформулированы две разные задачи и получены одинаковые решения. Первая задача: центру необходимо выбрать такую внутрифирменную цену, чтобы сумма затрат агентов была минимальна, при условии, что агенты выбирают свои действия из условия максимизации своих целевых функций. Вторая задача: найти оптимальный набор планов, таких, что сумма этих планов равна R, а сумма затрат агентов минимальна. В результате множитель Лагранжа в этой задаче – внутрифирменная цена 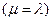. Интересно, что в данной модели оптимальной оказалась пропорциональная система стимулирования, и, более того, оптимальной оказалась система стимулирования, в которой ставки оплаты для всех агентов одинаковы (такая система стимулирования называется унифицированной). Ведь можно было бы каждому агенту назначать свою цену, но оптимальна одинаковая цена для всех агентов.

Известна следующая задача: выполняется некоторый проект и необходимо сократить критический путь (время выполнения проекта). Тогда тем агентам, кто выполняет критические операции, нужно дополнительно доплачивать, чтобы они сокращали время выполне­ния операций, а в сумме они должны сократить длительность проекта на заданную величину. Если участники проекта, выполняющие критические операции, имеют квадратичные затраты, а за единицу сокращения времени им платят 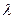, то получается такая же задача с аналогичным решением.

Естественно, результат, который мы получили: решения задач совпадают, оптимальным является система стимулирования, когда ставки всех агентов одинаковы (унифицированная система стимулирования) – справедлив только в рамках тех предположений, которые введены выше, а именно: в данной модели существенным является предположение о виде функций затрат агента (квадратичная функция). Это свойство степенных функций дает в экономико-математических моделях много хороших свойств:

1) оптимальность унифицированной системы стимулирования (оптимальность единой ставки оплаты);

2) возможность решения задач агрегирования, то есть, решая задачи минимизации затрат с данным набором агентов с характеристиками r_i, получили, что затраты на выполнение данного заказа имеют такой же вид, что и затраты одного агента с характеристикой H – все агенты могут быть заменены на одного агента, действие которого равно сумме их действий, и тип которого равен сумме их типов.

Такие свойства присущи квадратичным функциям, функциям типа Кобба-Дугласа: 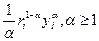. Это можно доказать и для функций более общего вида: 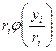, где 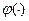– возрастающая выпуклая функция, равная нулю в нуле.

Выше считалось, что все параметры известны, и задача решалась в рамках предположения, что, в частности, известны параметры r_i функций затрат агентов. Рассмотрим задачу, когда информацией о типах агентов r_i центр не обладает. Обозначим s_i - сообщение i -го агента о своем типе.

Центр на основании сообщений агентов решает задачу планирования, то есть определяет, какими должны быть вектор планов x (s) и значение внутрифирменной цены 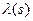в зависимости от сообщений агентов.

Первое, что приходит в голову - воспользоваться решениями задач, которые получены при полной информированности о функциях затрат агентов. То есть центр может подставить сообщения агентов в параметры механизмов, которые мы определили, решая задачу в условиях полной информированности, и назначать планы в соответствии с полученными механизмами.

Данный путь приведет к тому, что значение 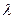будет следующим: 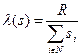, план, назначаемый i -му агенту будет равен (подставляем вместо типов сообщения): .

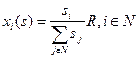Получили так называемый механизм внутренних цен, который похож на механизм пропорционального распределения ресурса. Но информация, сообщаемая центру, зависит от агентов. Рассмотрим их целевые функции, подставив в них зависимости 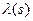и x_i (s)для того, чтобы понять, будет ли агенту выгодно выполнять назначенный план, и какую информацию ему будет выгодно сообщать:

.

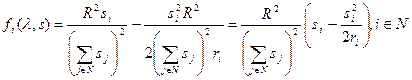Получили целевую функцию, которая зависит не от действий, а от сообщений агентов. Какие сообщения будет делать агент, чтобы максимизировать свою целевую функцию?

Будем искать максимум целевой функции i -го агента по его сообщению s_i. Для дифференцирования неудобен знаменатель, так как он тоже включает в себя s_i. Избавляются от этого «недостатка» введением гипотезы слабого влияния: предположим, что агентов достаточно много, то есть так много, что каждый агент своим сообщением практически не влияет на общий для всех агентов управляющий параметр – внутрифирменную цену. Знаменатель целевой функции тогда не будет зависеть от сообщения отдельного агента (сумма сообщений является «константой»). Получим, что 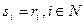, то есть сообщение достоверной информации выгодно всем агентам – механизм является неманипулируемым. Итак, для механизма внутренних цен выполняется:

1) требование сообщения агентами достоверной информации;

2) балансовое ограничение: сумма действий равна требуемой величине;

3) суммарные затраты агентов минимальны.