2014-02-02
3454
Пусть какой-то ресурс имеется у центра, и он необходим агентам. Задача центра – распределить его между агентами. Если центр знает эффективность использования ресурса подчиненными, то задача заключается в том, как распределить ресурс, например, чтобы суммарный эффект от его использования был максимальным. Если агенты являются активными, а центр не знает эффективности использования ресурса, и спрашивает у них: кому сколько ресурса нужно, и кто как будет его использовать, то, если ресурс ограничен, то агенты в общем случае не сообщат честно, кому сколько нужно, и ресурсов на всех не хватит. В каких ситуациях управляющий орган может предложить такую процедуру, то есть правило распределения ресурсов между агентами, которая была бы неманипулируема, то есть такую процедуру, чтобы каждому из агентов было выгодно говорить правду, независимо от того, сколько ресурса ему надо?
Рассмотрим механизм распределения ресурсов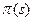 
, который обладает следующими свойствами:
1) процедура планирования непрерывна и монотонна по сообщениям агентов (монотонность означает, что чем больше просит агент ресурса, тем больше он его получает);
|
|
|
2) если агент получил некоторое количество ресурса, то он может, изменяя свою заявку, получить и любое меньшее количество ресурса;
3) если количество ресурса, распределяемое между группой агентов, увеличилось, то каждый из агентов этой группы получит не меньшее количество ресурсов, чем раньше.
Целевая функция агента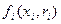 
зависит от типа ri данного агента, который в случае механизмов распределения ресурса будет рассматриваться как оптимальное количество ресурса для данного агента.
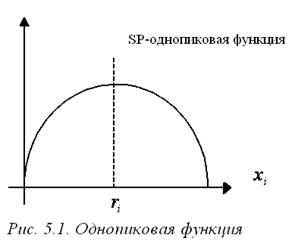
Допустим, что целевая функция агента имеет единственный максимум по xi в точке пика. То есть агенту нужно некоторое количество ресурса, если ему недодают ресурса – его полезность при этом меньше, если ему дают лишний ресурс – его полезность тоже меньше. Единственным максимумом может быть и бесконечность, то есть целевая функция может монотонно возрастать. Такие функции предпочтения называются однопиковые (см. рис. 5.1).
Рассмотрим сначала пример, а потом приведем общие результаты.
Пример 5.1. Пусть n= 3,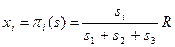 
, R – количество ресурса, 
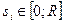. Пусть R =1; r 1 = 0,3; r 2=0,4; r 3=0,5. Имеем: r 1+ r 2+ r 3=1,2> R =1.
1) Пусть каждый агент сообщает правду, тогда:
;
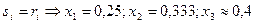2) Пусть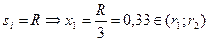 
. Первый агент решает задачу: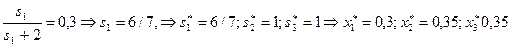 
Это - равновесие Нэша.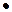
Приоритетные механизмы. В приоритетных механизмах распределения ресурса, как следует из их названия, при формировании планов (решении о том, сколько ресурса выделить тому или иному агенту) в существенной степени используются показатели приоритета агентов. Приоритетные механизмы в общем случае описываются следующей процедурой:
|
|
|
,
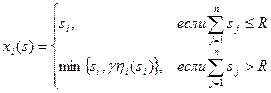где n - число агентов,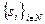 
- их заявки, 
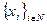- выделяемые количества ресурса, R - распределяемое количество ресурса, 
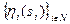- функции приоритета агентов, 
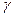- некоторый параметр.
Операция взятия минимума содержательно означает, что агент получает ресурс в количестве, не большем запрошенной величины. Параметр 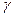играет роль нормировки и выбирается из условия выполнения балансового (бюджетного) ограничения:
то есть подбирается таким, чтобы при данных заявках и функциях приоритета в условиях дефицита распределялся в точности весь ресурс R.
Приоритетные механизмы, в зависимости от вида функции приоритета, подразделяются на три класса - механизмы прямых приоритетов (в которых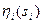 
- возрастающая функция заявки 
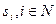), механизмы абсолютных приоритетов, в которых приоритеты агентов фиксированы и не зависят от сообщаемых ими заявок (Так как в механизмах абсолютных приоритетов планы, назначаемые агентам, не зависят от их заявок, то в рамках гипотезы благожелательности можно считать любой механизм абсолютных приоритетов неманипулируемым. Недостатком этого класса механизмов можно считать то, что в них центр никак не использует информации, сообщаемой агентами.) и механизмы обратных приоритетов (в которых 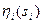– убывающая функция заявки 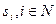). Рассмотрим последовательно механизмы прямых и обратных приоритетов.
Механизмы прямых приоритетов. Процедура распределения ресурса пропорционально заявкам, называется механизмом пропорционального распределения:
.
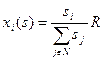Это – самый распространенный способ распределения ресурса. Видно, что данная процедура распределения ресурса удовлетворят условию нормировки. При любых комбинациях сообщений агентов распределяется в точности весь ресурс. Условия непрерывности и монотонности также выполнены.
Предположим, что сообщение каждого агента лежит в диапазоне от нуля до всего количества ресурсов, то есть, как минимум, агент может отказаться от ресурса, как максимум, может попросить весь ресурс, который имеется у центра.
Если агент получил некоторое количество ресурса, то, уменьшая заявку, в силу непрерывности и монотонности процедуры распределения ресурса, он всегда может получить меньшее количество, вплоть до нуля.
Если каждый агент скажет правду, сколько ему нужно, тогда он получит меньше, что логично, потому что ресурсов не хватает, агенты сказали правду и были «пропорционально урезаны».
Предположим, что игру центр разыгрывает неоднократно. На втором шаге агенты попросят больше. Если каждый будет просить максимально возможную заявку, то все получат поровну. Если кому-то этого много, то излишки он может отдать другому, но кому-то все равно не хватит.
Данный механизм является манипулируемым, потому что агентам невыгодно сообщать достоверную информацию о своих типах – тех количествах ресурса, которое им необходимо.
Итак, выше рассмотрен пример механизма распределения ресурса. Рассчитано равновесие. Запишем результаты исследования таких механизмов в общем виде. Для этого попробуем сначала понять, какими свойствами характеризуется равновесие. Агентов можно разделить на две категории:
1) «приоритетные» агенты (диктаторы) – те, кто получают абсолютно оптимальные для себя значения плана, то есть планы, равные их типам (при механизме распределения ресурса – те агенты, которые получают ресурса ровно столько, сколько им нужно),
2) «обделенные» агенты – те, кому не хватает ресурса, те, кто хоть и просит по максимуму, но в равновесии получает меньше, чем ему нужно.
Следующие два свойства характеризуют равновесие.
