Понятие устойчивости. Необходимые и достаточные условия устойчивости

Лекция 7. Устойчивость линейных систем

Управляемость и наблюдаемость

Линейную стационарную систему автоматического регулирования называют полностью управляемой, если из любого начального состояния ее можно перевести в конечное состояние при помощи входного сигнала в течение конечного интервала времени.

С понятием управляемости связано понятие наблюдаемости системы. Наблюдаемость позволяет установить начальное состояние системы автоматического регулирования по результатам измерения одного выходного сигнала.

Линейную стационарную систему автоматического регулирования называют полностью наблюдаемой, если можно определить ее начальное состояние по выходному сигналу, заданному на конечном интервале времени.

При оценке свойств спроектированной системы автоматичес­кого регулирования обычно, прежде всего, выясняют ее устойчи­вость. Это можно установить, исследуя свободное движение систе­мы, т. е. ее поведение под влиянием начальных условий.

Предположим, что на систему в течение некоторого промежутка времени, кроме задающего воздействия, действует возмущение и в ре­зультате состояние системы в момент t =t _о характеризуется начальными зна­чениями регулируемой величины и ее производ­ных. Предположим далее, что в момент времени t₀ влияние возму­щения прекращается. Следовательно, дальнейшее поведение си­стемы определяется задающим воздействием и начальными усло­виями у'(0),у²(0)..., у^n-1 (0), причем на основании принципа супер­позиции эти два влияния в линейной системе незави­симы одно от другого.

В наиболее благоприятном случае свободная составляющая регулируемой величины, которая создается начальными условиями, с течением времени стремится к нулю. Такую систему называют устойчивой.

Возможно также, что свободная составляющая стремится к не­которому конечному значению или совершает гармонические коле­бания, амплитуда которых стремится к некоторому конечному значению. Такие системы называют нейтральными (нейтрально устойчивыми).

Возможно, наконец, что свободная составляющая регулируе­мой величины неограниченно возрастает или совершает гармони­ческие колебания с неограниченно возрастающей амплитудой. Такие системы называют неустойчивыми.

Итак, система является устойчивой, если после прекращения внешнего воздействия она по истечении некоторого времени воз­вращается к тому состоянию равновесия или вынужденного дви­жения, в котором находилась до начала воздействия.

Оценка устойчивости системы есть оценка ее принципиальной способности осуществлять регулирование, поэтому с оценки устой­чивости начинают с исследование всякой системы.

Условие устойчивости. Пусть дифференциальное уравнение линейной или линеаризованной системы имеет следующий вид:

(а₀рⁿ + а₁р^n-1 + a_n-1 p + а_n) у = (b_op^m + b_lp^m-1 + …..+ b_m-1p + b_m)g + (c₀p^k +c₁p^k-1…..+ c _k-1p + c_k)f, (7.1)

где у = у (t), g = g (t) и f = f(t) — соответственно регулируе­мая величина, задающее воздействие и возмущение или отклоне­ния этих величин от их базисных значений; а₀, а₁..., а_n, b_о, b₁,…b_m, с₀, с₁,….с_k — постоянные коэффициенты; m ≤ n и k≤ n; р = d/dt - оператор дифференцирования.

Для оценки устойчивости системы должна быть исследована свободная составляющая решения уравнения (7.1), т. е. решение однородного уравнения

(а₀рⁿ + а₁р^n-1 + a_n-1 p + а_n) у = 0 (7.2)

при начальных условиях y(0) = y₀; y¹(0) = y¹₀; ….y^n-1(0) = y^n-1₀, где y₀, y¹₀,…. y^n-1₀ — постоянные, ограниченные по абсолютной величине.

Общее решение однородного уравнения (7.2) есть сумма сла­гаемых, вид которых определяется значениями корней характе­ристического уравнения

D = а₀рⁿ + а₁р^n-1 + a_n-1 p + а_n = 0 (7.3)

Следует заметить, что коэффициенты уравнения (7.3) и, сле­довательно, значения его корней зависят только от параметров системы — от свойств и параметров ее элементов, способа их соединения.

Если характеристическое уравнение САР не имеет кратных корней (что наиболее вероятно, когда корни вычи­сляют приближенно), то решение уравнения (7.2) будет иметь сла­гаемые вида

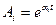и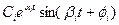

Первое слагаемое соответствует вещественному корню α, а второе - паре сопряженных комплексных корней α ± jβ, где А_i, C_i и ψ_i – постоянные интегрирования, зависящие от начальных условий и ограниченные по величине.

При исследовании решения уравнения (7.2), если какое-ни­будь его слагаемое неограниченно возрастает по абсолютной ве­личине, то обязательно неограниченно возрастает по абсолютной величине и вся сумма в целом (независимо от наличия членов с раз­ными знаками).

Очевидно, что присутствие одного положительного веществен­ного корня α_i > 0 достаточно для того, чтобы соответствующее ему слагаемое в решении уравнения (7.2) неограниченно возрастало по абсолютной величине. При наличии одной пары сопряженных комплексных корней с положительной вещественной частью α_i > 0 в решении уравнения (7.2) оказывается гармоническое сла­гаемое с неограниченно возрастающей амплитудой. В обоих слу­чаях система оказывается неустойчивой.

Таким образом, для устойчивости линейной системы необходимо и достаточно, чтобы все корни ее характеристического уравнения имели отрицательную вещест­венную часть. При наличии хотя бы одного корня с положительной вещественной частью система неустойчива.

Среди корней характеристического уравнения может быть ко­рень, равный нулю α_i = 0 или пара чисто мнимых корней ± jβ. Если при этом вещественные части всех остальных корней отрица­тельные, то решение уравнения (7.2) будет иметь соответственно постоянное слагаемое A_i или гармоническое слагаемое с постоян­ной амплитудой C_isin(β_it + ψ_i). В этих случаях система находится на границе устойчивости и относится к неустойчивым системам. Последнее утверждение действительно для линейных систем.

Сформулированное выше условие устойчивости справедливо как для линейных, так и для линеаризованных систем: по корням характеристического уравнения системы, элементы которой описываются линеаризованными уравнениями, действительно можно судить о ее устойчивости. Однако в случае нулевых или чисто мнимых корней характеристического уравнения линеаризованной системы вопрос об устойчивости может быть решен только на основании исследования ее нелиней­ных уравнений.

Корни алгебраического уравнения, как и всякие комплексные числа, удобно представлять в виде точек на комплексной плос­кости. Для устойчивости линейной системы необходимо и доста­точно, чтобы все корни характеристического уравнения лежали слева от мнимой оси комплексной плоскости (рис. 7.1, а), или все корни были «левыми».

Если хотя бы один вещественный корень или одна пара сопря­женных комплексных корней находится справа от мнимой оси, то система неустойчива (рис. 7.1, б).

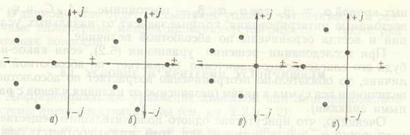
Рис. 7.1. Расположение корней характеристического уравнения системы пятого порядка:

а -- устойчивой; 6 — неустойчивой; в и г - находящейся на границе устойчи­вости.

Мнимая ось является, следовательно, границей устойчивости. Говорят, что система находится на границе устойчивости, если имеется нулевой корень (рис. 7.1, в) или пара чисто мнимых кор­ней (рис. 7.1, г), а остальные корни «левые».

На практике для упрощения вычислений устойчивость систем определяют с помощью некоторых критериев без вычисления кор­ней характеристического уравнения. Критерий устойчивости — это математическая формулировка условий, которым удовлетво­ряют коэффициенты характеристического уравнения устойчивой системы. Критерии устойчивости эквивалентны по содержанию, сформулированному выше условию устойчивости.

Мы ограничимся рассмотрением алгебраических критериев устойчивости Гурвица и Рауса и ча­стотных критериев Михайлова и Найквиста.

Критерий Гурвица удобен для исследования устойчивости си­стем третьего и четвертого порядков, когда известны параметры системы. Кроме того, он позволяет получить аналитическое выра­жение (выражения) для границ области возможных значений какого-либо параметра (параметров) системы, при которых сохра­няется устойчивость.

Критерий Рауса широко используют при определении устойчи­вости систем высокого порядка, если известны числовые значе­ния коэффициентов его характеристического уравнения. Этот кри­терий удобен при использовании ЭВМ. При этом возникает возможность выяснить влияние коэффициентов уравнения или параметров системы на ее устойчивость.

При использовании критерий Михайлова, кроме определения устойчивости, легко установить, в каких пределах можно изме­нять тот или иной параметр системы.

По критериям Гурвица, Рауса и Михайлова можно судить об устойчивости системы, как в замкнутом, так и в разомкнутом состоянии. Критерий устойчивости Найквиста используется для определения устойчивости замкнутых систем по АФЧХ разомкнутой системы.

Критерий Найквиста наиболее широко используют по следую­щим причинам:

1. Устойчивость замкнутой системы исследуют по частотной передаточной функции ее разомкнутой цепи, а эта функция чаще всего состоит из простых сомножителей. Коэффициентами являются реальные параметры системы, что позволяет выбирать их из усло­вия устойчивости.

2. Для исследования устойчивости можно использовать экспе­риментальные частотные характеристики наиболее сложных элементов системы (объект регулирования, исполнительный элемент), что повышает точность полученных результатов.

3. Исследовать устойчивость можно по логарифмическим ча­стотным характеристикам, построение которых не требует трудоем­ких расчетов.

4. Удобно определять запас устойчивости.

При использовании критериев Гурвица, Рауса и Михайлова для исследования устойчивости системы рассматривают ее харак­теристическое уравнение.