2014-02-02
1228
Частотные методы исследования устойчивости.
Частотные методы исследования устойчивости основаны на связи расположения корней полинома Р(р) и годографом этого полинома на комплексной плоскости, т.е. графиком комплексно-значной функции Р(jw) при изменении w от 0 до ¥.
Основным теоретическим результатом является критерий Михайлова. Этот критерий формулируется в виде условия на полином, а его следствия, например, критерий Найквиста, уже формулируются в виде требований к передаточным функциям, что имеет непосредственное применение.
· Необходимое и достаточное условие. Критерий Михайлова
(А.В.Михайлов, Москва 1938г.)
Годограф устойчивого полинома n – го порядка с положительными коэффициентами (ак>0), начинаясь на положительной вещественной полуоси, последовательно проходит n/2 квадрантов, поворачиваясь против часовой стрелки. Приращение аргумента 
Dj = np / 2.
Нарушение любой части этого условия приводит к неустойчивости.
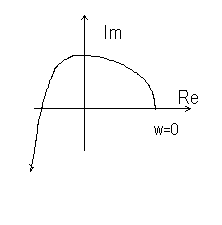
Это пример устойчивого годографа для полинома порядка 3.
Из критерия Михайлова вытекает простое правило перемежаемости (чередуемости) корней. В самом деле, из рисунка видно, что корни мнимой и вещественных частей при увеличении w сменяют друг друга в строгой последовательности, запишем это условие в явном виде:
;
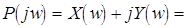
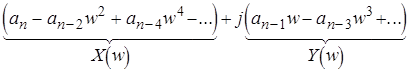Найдем корни отдельно вещественной и отдельно мнимой части и расположим их в порядке возрастания: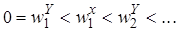 
- правило чередования корней.
Применим для полинома третьего порядка:
= 
;
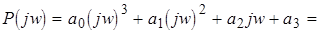
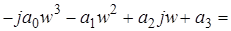
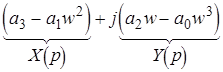Корни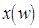 
: 
; 
;
: 
; 
; 
;
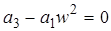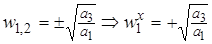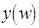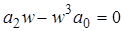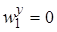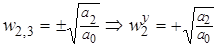Условие чередования даёт: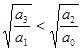 
т.е a1 a2 > a0 a3, это же вытекает для системы 3 порядка и из критерия Гурвица.
Отметим, что преимущество применения правила перемежаемости – более простые полиномы (только чётного и только нечётного порядка).
· Критерий устойчивости замкнутой системы - критерий Найквиста.
Позволяет исследовать устойчивость замкнутой системы (всей САУ) по частотной характеристике разомкнутой системы.
Определение: разомкнутой системой являются все последовательно соединенные блоки от входа системы до точки замыкания обратной связи.
Wрс(p) = W(p) Wос(p)
АФЧХ разомкнутой САУ имеет вид: Wpc(j
)
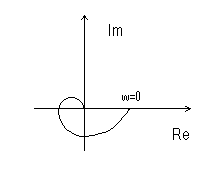
Критерий Найквиста связывает устойчивость замкнутой системы с поведением частотной характеристики и годографа разомкнутой системы. Доказывается с помощью двукратного применения критерия Михайлова:
Один раз - к разомкнутой системе (устойчивой или неустойчивой), другой раз - к замкнутой системе (только устойчивой).
Если разомкнутая система устойчива, то имеем следующий критерий:
Для устойчивости замкнутой системы необходимо и достаточно, чтобы годограф устойчивой разомкнутой системы “не охватывал” точку
(-1; j0).
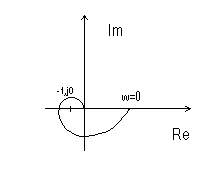
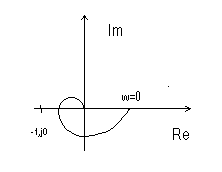
годограф охватывает (-1,,j0) годограф не охватывает (-1,,j0)
Уточнение понятия ”охват точки” (-1; j0) годографом Найквиста:
Так как понятие охвата является нечетко сформулированным, вводим абсолютно точное правило переходов:
