Суть метода

Метод гармонической линеаризации

Сущность метода гармонической линеаризации заключается в отыскании периодического решения на входе нелинейного элемента, разложении сигнала на выходе нелинейного элемента в ряд Фурье и его замене первой гармоникой. Такая замена справедлива, если линейная часть системы автоматического регу­лирования является фильтром низких частот, хорошо гасящим колебания высших гармоник.

Метод применим для исследования нелинейных систем любого порядка и при наличии нескольких нелинейностей. Однако мы ограничимся рассмотрением НС вида, изображенного на рис.10.1.

Уравнение линейной части системы в общем виде запишем

Q(p)y = R(p)U,

а уравнение НЭ

U = F(d) = F(y), если g = 0,

где F(y) – заданная нелинейная функция, y – переменная на входе нелинейного элемента.

Метод гармонической линеаризации применим и к более сложным нелинейным уравнениям вида U = F(y,dy), d²U + F(dU,U) = ky и т.д.

Поставим задачу отыскания автоколебаний в данной нелинейной системе. Автоколебания имеют, строго говоря, несинусоидальную форму. Однако можно считать, что для переменной «у» они близки к синусоидальной из-за того, что линейная часть системы не пропускает колебания с высокими частотами. Поэтому будем искать автоколебания переменной «у» приближенно в виде синусоиды

у = а*sinwt, (10.1)

где а и w искомые амплитуда и частота автоколебаний.

Подставляя значение «у» в заданную нелинейную функцию U = F(y), разложим ее в ряд Фурье:

U=F(y)=C₀+D₁sinwt+C₁coswt+D₂sin2wt + C₂cos2wt +... (10.2)

где C₀, D₁, C₁, D₂, C₂….- коэффициенты ряда Фурье.

Положим, что постоянная составляющая в искомых колебаниях отсутствует, т.е. С₀ = 0. Это условие удовлетворяется всегда, когда нелинейная характеристика симметрична относительно начала координат и отсутствует внешнее возмущающее воздействие.

Можно находить колебания и при наличии постоянной составляющей, но тогда решение надо искать в виде у = у₀+а*sinwt.

В уравнении (10.2) произведем замену согласно (10.1)

sinwt = у/а и coswt = ру/(аw) (10.3)

и отбросим все высшие гармоники ряда Фурье, полагая, что они не пропускаются линейной частью системы.

В выражении (10.3) ру – производная.

Тогда уравнение НЭ для первой гармоники выходной величины с учетом (10.2) и (10.3) примет вид

U = 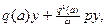(10.4)

где q(a) и q¹(a) – коэффициенты, определяемые формулами:

q(a) =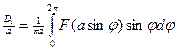

q¹(a) =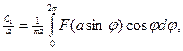

где j = wt.

В результате нелинейное уравнение U = F(y) заменяется приближенным уравнением для первой гармоники, похожим на линейное уравнение. Особенность его заключается в том, что коэффициенты уравнения зависят от амплитуды и частоты искомых автоколебаний. Замена уравнения (10.1) уравнением (10.4) называется гармонической линеаризацией, а коэффициенты q(a) и q¹(a) называются коэффициентами гармонической линеаризации нелинейного элемента.

Тогда передаточная функция нелинейного гармонически линеаризованного звена имеет вид:

W_н(а, w) =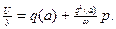

Используя уравнения линейной части и приближенное уравнение нелинейного звена получим характеристическое уравнение замкнутой системы в виде

Q(p) + R(p)[q(a) + pq¹(a)/ w = 0. (10.5)

Задача состоит в нахождении периодического решения у = а*sinwt, т.е. в определении из уравнения (10.5) амплитуды а и частоты колебаний w. Однородное линейное уравнение может иметь такое решение только тогда, когда характеристическое уравнение имеет пару чисто мнимых корней.