Применение критерия Михайлова для определения автоколебаний и устойчивости

Выражение кривой Михайлова для характеристического уравнения (10.5) имеет вид:

F(jw) = Q(jw) + R(jw)[q(a) + jwq¹(a)/W].

Здесь для исключения путаницы текущего параметра w с искомой частотой автоколебаний обозначили ее через W.

В последнем выражении выделим вещественную и мнимую части F(jw) = X(W,w,a) + jY(W,w,a).

Величины W и a входят здесь в коэффициенты выражения кривой Михайлова.

Чтобы характеристическое уравнение имело чисто мнимые корни, годограф Михайлова должен проходить через начало координат, причем, как известно, значение w в начале координат определяет частоту колебаний W. Значит, при W = w должны одновременно равняться нулю обе координаты: х = 0 и у = 0. Отсюда получаем два уравнения

Х(W,а) = 0; У(W,а) = 0, (10.6)

из которых и определяются две неизвестные а и W, т.е. амплитуда и частота периодического решения у = аsinWt, которая может иметь место в данной нелинейной системе.

Если уравнение (10.6) дает вещественные положительные ответы для а и W, то это значит, что в системе имеется периодическое решение. Если же нет, то в системе нет периодических решений.

Однако аналитически найти решение уравнений (10.6) удается не всегда и поэтому прибегают к графическим или графоаналитическим приемам решения.

Необходимо иметь в виду, что если получено определенное периодическое решение у = аsinWt, то это еще не обязательно соответствует автоколебаниям в системе. Поэтому после отыскания периодического решения необходимо проверить, является ли оно устойчивым или нет, т.е. сходится ли переходный процесс к периодическим колебаниям.

Учитывая, что при наличии периодического решения кривая Михайлова проходит через начало координат, устойчивость периодического решения можно определить следующим образом. Увеличивают амплитуду периодического решения на величину Dа. Тогда годограф Михайлова отклонится от начала координат в ту или другую сторону (см. рис.10.10). Если он отклонится в положение 1, то имеют место затухающие колебания, если же в положение 2, то – расходящиеся колебания.

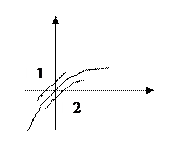Рис.10.10. Деформация годографа Михайлова при различных приращениях амплитуды

Для устойчивости периодического решения годограф Михайлова должен отклоняться в положение 1 при Dа > 0 и в положение 2 при Dа < 0. Это геометрическое условие устойчивости периодического решения можно записать аналитически в виде

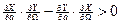, (10.7)

где в частные производные должны быть подставлены значения а и W = w того периодического решения, устойчивость которого исследуется.

Если же неравенство (10.7) не удовлетворяется, то имеет место неустойчивое периодическое решение.