Абсолютная устойчивость нелинейных систем

При расчетах систем автоматического регулирования встречаются та­кие задачи, когда требуется исследовать динамику процессов регулирования в условиях отсутствия сведений о характеристиках отдельных устройств. Особенно часто бывают неизвестны нелинейные характеристики исполни­тельных устройств систем. При исследовании устойчивости таких систем независимо от вида нелинейной характеристики пользуются понятием абсо­лютной устойчивости.

Анализ абсолютной устойчивости систем регулирования выполняется с помощью структурной схемы (рис. 10.1) с разделенными линейной и нелинейной частями. В общем случае нелинейный элемент описывается функциональной зависимостью U=F (D).

Характеристики, описываемые этими соотношениями, могут иметь самую разнообразную форму, однако все они должны быть расположены внутри сектора, ограниченного двумя прямыми, проходящими через начало координат (рис. 10.11).

Рис.10.11. Область нахождения нелинейности

Иначе говоря, должно соблюдаться условие r £ U/D £ k

для всех точек нелинейности. Здесь r = tga, a k = tgb.

Рассмотрим систему при таких воздействиях, которые ограничены по модулю и являются исчезающими функциями времени. Обозначим максимальное воздействие sup|g(t)|.

Исчезающей функцией времени g(t) назовем функцию, стремящуюся с течением времени к нулю: limg(t) = 0 при t ® ¥.

Положение равновесия устойчиво, если существует такое положительное число l(А) > 0, что при sup|g(t)| = l(А) имеет место неравенство |D(t)| £ A, где А – сколь угодно малое число.

В зависимости от того, при каких значениях l(А) выполняется неравенство |D(t)| £ A, различают три вида устойчивости. Устойчивость в малом, если l(А) бесконечно малая величина; устойчивость в большом, если l(А) конечная величина; и у стойчивость в целом, если l(А не ограничена.

Абсолютной устойчивостью называют устойчивость положения равновесия в целом.

Наиболее разработанными являются методы исследования абсолютной устойчивости для рассмотренных нелинейностей. Такие нелинейности еще называют нелинейностями, принадлежащими сектору (r,k).

Для анализа абсолютной устойчивости нелинейной системы румынским ученым В. М. Поповым предложен частотный критерий, определяющий достаточные условия устойчивости. Работы В. М. Попова явились основополагающими для нового направления в иссле­довании абсолютной устойчивости нелинейных систем, связанного с исполь­зованием частотных представлений, широко распространенных при анализе и синтезе линейных систем. Основное достоинство этого метода заключается в том, что он пригоден для анализа нелинейных систем высокого порядка. При использовании этого метода рассматриваются нелинейности класса (0,k).

В методе используется видоизмененная частотная характеристика линейной части системы, которая перестраивается из W(jw), если не менять вещественную частотную характеристику, а мнимую частотную характеристику умножить на w

W^*(jw) = Re W(jw) + jwIm W(jw) = U(w) +jV^*(w).

Критерий Попова следует из теоремы: для того, чтобы система с нелинейностью, принадлежащей сектору (о,k) была абсолютно устойчива, достаточно, чтобы можно было подобрать такое конечное число q, при котором при любом w ³ 0 выполнялось неравенство

Re[1 +jqw]W(jw) + 1/k = ReW(jw) -qwImW(jw) + 1/k.

Тогда условие устойчивости будет иметь вид:

U =qV + 1/k ³ 0.

Уравнение U =qV + 1/k = 0 определяет в плоскости U, V прямую, проходящую через точку U = -1/k, V = 0 с угловым коэффициентом 1/q.

Критерий абсолютной устойчивости сформулирован В.М. Поповым следующим образом: для абсолютной устойчивости достаточно, чтобы в плоскости UV через точку действительной оси с абсциссой -1/к можно было провести негоризонтальную прямую, так чтобы видоизмененная частотная характеристика W^*(jw) не пересекала этой прямой (она может иметь с этой прямой общие точки).

На рисунке 10.12 изображены АФЧХ W^*(jw) различных систем.

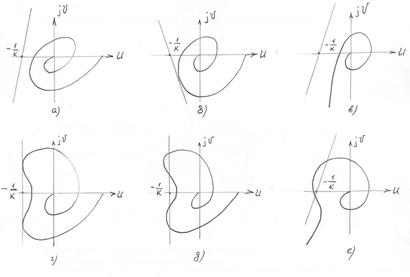
Рис.10.12. Различные варианты устойчивости систем согласно критерия устойчивости Попова

На рис.10.12,а – г изображены АФХ W^*(jw) абсолютно устойчивых систем, для которых критерий устойчивости Попова выполняется, на рис.10.12,д,е – характеристики неустойчивых систем, для которых этот критерий не выполняется.