Метод фазовой плоскости

Метод фазовой плоскости в теорию автоматического регулирования был введен А. А. Андроновым. Сущность метода заключается в построении фазовых траекторий по дифференциальным уравнениям в системе координат: отклонение регулируемой величины х и скорость ее изменения y = dx/dt.

Это наиболее распространенный выбор координат фазовой плоскости. Вообще же можно использовать любые две переменные.

Процесс изменения траектории представляет собой движение изображающей точки на плоскости. Начальные условия системы определяют первоначальное положение изображающей точки на фазовой плоскости. Совокупность фазовых траекторий в плоскости (х, у) представляет собой фазовый портрет.

Фазовые портреты различных процессов изображены на рис.10.4 – 10.8.

Рис.10.4 соответствует случаю периодических колебаний с постоянной частотой и амплитудой.

Рис.10.5 – затухающему, а рис.10.6 - колебательному расходящемуся процессу. Рис.10.7 – затухающим к нулю, а рис.10.8 - расходящимся апериодическим процессам.

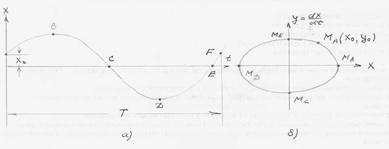
Рис.10.4. Периодические колебания и ее фазовый портрет

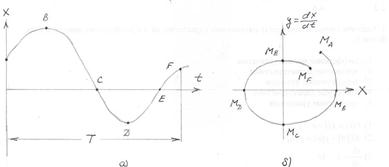
Рис.10.5. Периодические затухающие колебания и ее фазовый портрет

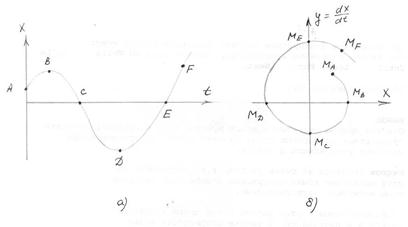
Рис.10.6. Периодические расходящиеся колебания и ее фазовый портрет

На основании приведенных рисунков можно заключить, что любой периодический колебательный процесс с постоянной амплитудой и частотой изображается на фазовой плоскости в виде некоторого замкнутого контура – замкнутой фазовой траектории. Каждому периоду колебаний соответствует прохождение изображающей точкой всего контура.

Затухающий колебательный процесс изображается на фазовой плоскости в виде сходящейся, а расходящийся в виде расходящейся спиралевидной фазовой траектории.

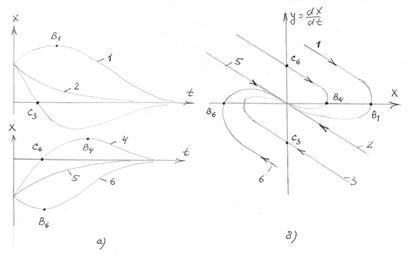
Рис.10.7. Затухающие к нулю апериодические процессы и их фазовые портреты

Затухающему к нулю апериодическому процессу соответствует вливающаяся в начало координат фазовой плоскости фазовая траектория, а расходящемуся апериодическому процессу - уходящая от начала координат фазовая траектория.