Краткосрочном периоде. Изопрофиты

Максимизация прибыли с одним переменным фактором в

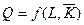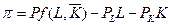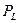В краткосрочном периоде производственная функция имеет вид кривой общего продукта , если . Функция экономической прибыли , где и 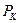- цены соответственно труда и капитала. Выразим выпуск как функцию переменной величины – затрат труда. Получим уравнение изопрофитной линии 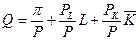, в которой всем комбинациям 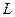, 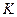и 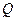соответствует постоянный уровень прибыли .

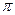Наклон изопрофитной линии равен 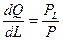. Условие максимизации прибыли 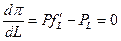. По мере изменения величины прибыли имеем семейство изопрофитных линий – параллельных прямых с наклоном 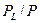. Величина 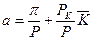измеряет сумму реальной прибыли и постоянных издержек . Более высокие уровни прибыли отмечаются на выше расположенных изопрофитах.

Задача максимизации прибыли сводится к нахождению самой высокой точки 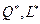на кривой общего продукта 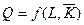и самой высокой изопрофитной линии. В этой точке наклоны названных линий будут равны. Так как наклон 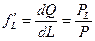кривой общего продукта измеряет предельный продукт 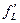, то 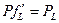, что эквивалентно условию максимизации прибыли.

Если повышается цена труда, то увеличивается и наклон кривой (рис. 3.7). На линии 2 с более высоким наклоном затраты труда уменьшаются, т.е. рост цены труда ведет к сокращению потребления труда фирмой.

Допустим, растет цена продукта, тогда снижается наклон изопрофитной линии и выпуск растет. Это свидетельствует о прямой зависимости между предложением и ценой товара, что подтверждает действие закона предложения.

Если изменяется цена капитала 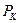, то в коротком периоде его потребление не изменится. Изменение цены капитала не изменяется наклон изопрофитной линии, не изменяются затраты труда 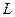и выпуск 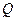, но изменяется прибыль фирмы.