Правило минимизации издержек фирмы

Изокоста - прямая равных издержек.

В соответствии с производственной функцией фирма стремится произвести максимальный объем продукции. Но существуют ограничения: цены факторов производства (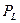– цена труда, 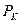– цена капитала) заданы рынком, – общие издержки фирмы. Фирма расходует все имеющиеся в ее распоряжении средства на покупку труда в количестве 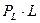и капитала в количестве . Тогда бюджетное ограничение производителя имеет вид: 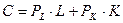или 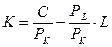. Это уравнение изокосты (isocost line) (рис. 3.15 а). Ее наклон отрицателен и равен 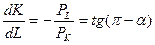– соотношению цен факторов производства. Точки на изокосте представляют все возможные сочетания затрат факторов производства, имеющие одинаковую рыночную стоимость.

При перемещении изокосты 2 (рис. 3.15а) в положение линии 3 цена капитала растет. На линиях 1 и 2 цены труда и капитала одинаковы. Фирма может производить продукцию (рис. 3.15б) в точке 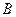в объеме 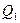или в точке 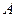в объеме 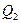. Выпуск 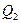- максимально возможный. В точке 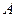изокоста касается изокванты. В этой точке наклон изокосты равен наклону изокванты. Наклон изокванты измеряется предельной нормой технологического замещения , а наклон изокосты . 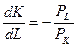Приравняв наклоны изокосты и изокванты, получим условие минимизации издержек: 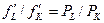или 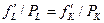. В случае выполнения условия средние общие издержки фирмы будут минимальными, так как при заданном объеме использованных ресурсов в денежной форме получен максимально возможный объем выпуска.

В определении величины затрат труда и капитала, при которых для заданного объема выпуска издержки на единицу продукции будут минимальными, используется следующий простой метод решения задачи. Издержки фирмы составляют 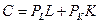, задан объем выпуска . Выразим затраты труда как функцию выпуска и затрат капитала 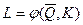. Функция издержек принимает вид: 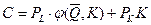. Решаем задачу на нахождение минимального значения 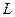и 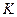для заданного выпуска классическим методом математического анализа. Приравняем к нулю первую производную функцию издержек и из полученного уравнения находим величину затрат капитала . Проверим, выполняется ли достаточное условие минимизации. Из 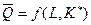находим значение затрат труда 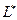. Затраты 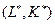обеспечивают минимум средних валовых издержек. Однако этот простой метод не всегда применим. Форма производственной функции не всегда позволят выразить затраты труда через затраты капитала и заданный выпуск. В общем случае используется метод Лагранжа.

Издержки производства минимизируем при ограничении . Функция Лагранжа имеет вид: 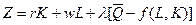, где 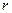- цена капитала, 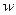- цена труда. Необходимые условия минимизации издержек:

Разделив первое уравнение на второе, получим 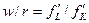. Это соотношение и есть условие минимизации издержек. Из выражения определим экономический смысл множителя Лагранжа в задаче минимизации издержек. Он показывает, на какую величину изменяются издержки при увеличении выпуска на единицу, т.е. характеризует величину предельных издержек.