Точки перегиба, Выпуклость, вогнутость линии

Дуга кривой называется выпуклой, если она пересекается с любой своей секущей не более, чем в двух точках.Выпуклость дуги может быть направлена или вверх (в направлении оси Оу), или внизЛинии, обращенные выпуклостью вверх, условились называть выпуклыми, а обращенные выпуклостью вниз – вогнутыми.

Необходимое условие выпуклости дуги: есть дуга линии y=f(x) выпукла на (a, b), то 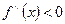при .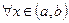

Необходимое условие вогнутости дуги: если дуга линии y=f(x) вогнута на (a, b), то 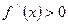при .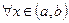

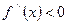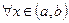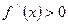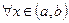Достаточное условие выпуклости, вогнутости дуги: если при , то дуга кривой y=f(x) выпукла на (a, b); если при , то дуга кривой y=f(x) вогнута на (a, b).

Точка С линии, отделяющая выпуклую дугу от вогнутой или наоборот, называется точкой перегиба.

Предполагается, что в точке перегиба можно провести касательную к данной линии, которая лежит при этом по обе стороны от касательной

Cлева от х = х₀ 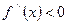, а справа 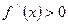. Это значит, что слева функция убывает, а справа возрастает. Интервалы монотонности меняются в точке, в которой производная функция равна нулю 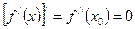или 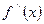не существует. Точка х = х₀ называется при этом критической.

Рассмотренное условие является лишь необходимым условием существования точки перегиба.Достаточное условие существования точки перегиба: если 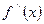меняет свой знак при переходе через критическую точку х = х₀, то точка 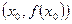- точка перегиба кривой y = f(x). Знаки 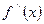слева и справа от х = х₀ показывают, как направлена выпуклость кривой при x < x₀ и x > x₀.