Пусть в электрической цепи с резистивным (активным) R, индуктивным L и емкостным С элементами (рис. 5.19) ток изменяется по синусоидальному закону:
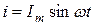 . (5.33)
. (5.33)
Рис.5.19
Уравнение электрического состояния для мгновенных значений напряжений имеет вид:
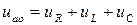 , (5.34)
, (5.34)
где 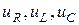 – падения напряжений на резистивном, индуктивном и емкостном элементах, соответственно.
– падения напряжений на резистивном, индуктивном и емкостном элементах, соответственно.
Согласно (5.6) напряжение на резистивном элементе 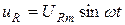 и совпадает по фазе с током
и совпадает по фазе с током  . Согласно (5.8) напряжение на индуктивном элементе
. Согласно (5.8) напряжение на индуктивном элементе 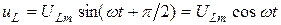 и по фазе опережает ток
и по фазе опережает ток  на угол
на угол 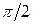 . Согласно (5.24) напряжение на емкостном элементе
. Согласно (5.24) напряжение на емкостном элементе 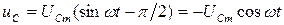 и по фазе отстает от тока
и по фазе отстает от тока  на угол
на угол 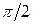 . Подставив значения напряжений на элементах в (5.34), получим:
. Подставив значения напряжений на элементах в (5.34), получим:
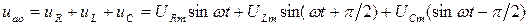 . (5.35)
. (5.35)
Выразив амплитудные значения напряжения на элементах через амплитуду тока 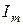 и значения резистивного и реактивных сопротивлений, преобразуем (5.35) к виду:
и значения резистивного и реактивных сопротивлений, преобразуем (5.35) к виду:
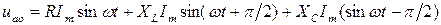 или
или
 . (5.36)
. (5.36)
Выражение (5.36) позволяет определить напряжение на входе цепи (рис.5.19) при известном токе (5.33) и сопротивлениях элементов.
Уравнение электрического состояния в векторной форме имеет вид:
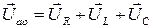 , (5.37)
, (5.37)
где 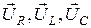 – падения напряжений на резистивном, индуктивном и емкостном элементах, соответственно. Построим векторную диаграмму (рис.5.20,а) для рассматриваемой цепи. Совместим вектор тока с осью абсцисс, т.к. начальная фаза тока (5.33) равна нулю. При этом вектор напряжения
– падения напряжений на резистивном, индуктивном и емкостном элементах, соответственно. Построим векторную диаграмму (рис.5.20,а) для рассматриваемой цепи. Совместим вектор тока с осью абсцисс, т.к. начальная фаза тока (5.33) равна нулю. При этом вектор напряжения 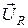 на резистивном элементе совпадает с вектором тока, вектор напряжения на индуктивном элементе
на резистивном элементе совпадает с вектором тока, вектор напряжения на индуктивном элементе 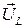 опережает ток на
опережает ток на 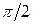 , а на емкостном элементе
, а на емкостном элементе 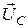 отстает от тока на
отстает от тока на 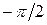 . Соединим начало вектора напряжения
. Соединим начало вектора напряжения 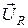 с началом координат (началом вектора тока). Начало вектора напряжения на индуктивном элементе
с началом координат (началом вектора тока). Начало вектора напряжения на индуктивном элементе 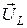 совместим с концом вектора напряжения
совместим с концом вектора напряжения 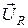 и развернем его на угол
и развернем его на угол 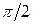 . Далее совместим начало вектора напряжения на емкостном элементе
. Далее совместим начало вектора напряжения на емкостном элементе 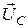 с концом вектора
с концом вектора 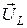 и повернем его на угол
и повернем его на угол 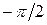 относительно вектора тока (на рис.5.20,апринято, что напряжение на емкостном элементе меньше напряжения на индуктивном элементе). Соединив конец вектора
относительно вектора тока (на рис.5.20,апринято, что напряжение на емкостном элементе меньше напряжения на индуктивном элементе). Соединив конец вектора 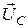 с началом координат, получим вектор напряжения
с началом координат, получим вектор напряжения 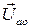 приложенного к цепи (вектор напряжения источника).
приложенного к цепи (вектор напряжения источника).
Рис.5.20,а Рис.5.20,б
Векторы 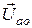 ,
, 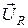 и
и 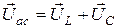 образуют прямоугольный треугольник напряжений, из которого получим:
образуют прямоугольный треугольник напряжений, из которого получим:
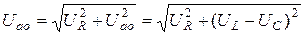 . (5.38)
. (5.38)
Поделив в (5.38) напряжение на ток, получим выражение для полного сопротивления рассматриваемой цепи:
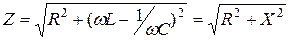 , (5.39)
, (5.39)
где 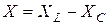 – реактивное сопротивление электрической цепи. Выражению (5.39) соответствует треугольник сопротивления цепи, приведенный на рис.5.20,б. Индуктивное и емкостное сопротивления характеризуют свойства цепи, обусловленные ее реакцией на изменение тока. Поэтому их называют реактивными.
– реактивное сопротивление электрической цепи. Выражению (5.39) соответствует треугольник сопротивления цепи, приведенный на рис.5.20,б. Индуктивное и емкостное сопротивления характеризуют свойства цепи, обусловленные ее реакцией на изменение тока. Поэтому их называют реактивными.
Из треугольника сопротивлений можно определить угол сдвига 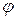 между током и напряжением используя выражения:
между током и напряжением используя выражения:
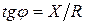 или
или 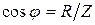 .
.
Активная (средняя) мощность характеризующая выделение энергии на активном сопротивлении цепи (резистивном элементе):
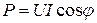 ;
;
Реактивная мощность характеризующая интенсивность обмена энергией между источником и реактивными элементами:
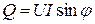 ;
;
Полная мощность:
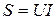 .
.
 2014-02-02
2014-02-02 1941
1941








