Условная вероятность. Теория вероятности как механизм представления неопределенности

Теория вероятности как механизм представления неопределенности

Условная вероятность события d при данном s — это вероятность того, что событие d наступит при условии, что наступило событие s. В традиционной теории вероятностей для вычисления условной вероятности события d при данном s используется следующая формула:

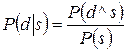
Как видно, условная вероятность определяется в терминах совместимости событий. Она представляет собой отношение вероятности совпадения событий d и s к вероятности появления события s. Из формулы следует, что

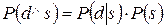
Если разделить обе части на P(s) и подставить в правую часть предыдущей формулы, то получим правило Байеса в простейшем виде:

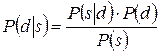
Это правило, которое иногда называют инверсной формулой для условной вероятности, позволяет определить вероятность P(d|s) появления события d при условии, что произошло событие s через известную условную вероятность P(s|d). В полученном выражении P(d) — априорная вероятность наступления события d, a P(d|s) — апостериорная вероятность, т.е. вероятность того, что событие d произойдет, если известно, что событие s свершилось.

Негативное отношение многих специалистов по искусственному интеллекту к вероятностному подходу обусловлено рядом причин:

- для вычисления условной вероятности P(d|s) нужно знать как вероятность события s и вероятность совместного события d ^ s, а такая информация как правило отсутствует;

- в большинстве классических работ по теории вероятностей понятие вероятности определялось как объективная частотность (частота появления при достаточно продолжительных независимых испытаниях).

Однако существует мнение, что эти базовые предположения небесспорны с точки зрения практических приложений. Сторонники такого подхода придерживаются субъективистской точки зрения на определение вероятности, который позволяет иметь дело с оценками совместного появления событий, а не с действительной частотой. Такой взгляд на вещи связывает вероятность смеси событий с субъективной верой в то, что событие действительно наступит.

Вычисление P(d|s) не вызывает затруднений в простейшем случае, когда множество S имеет размерность 1. Если же в множестве D имеется m членов, а в множестве S — n членов, потребуется вычислить mn + m + n оценок вероятностей.

Ситуация значительно усложняется, если мы пробуем включить в оценку каждого события из множества D не одно, а несколько событий из S. В более общей форме правило Байеса имеет вид:

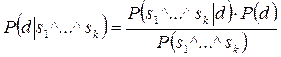
и требует вычисления (mn)^k + m + n^k оценок вероятностей, что даже при небольшом значении k очень много. Однако, если предположить независимость событий s объем вычислений существенно снижается.

Таким образом, использование теории вероятности ставит перед нами следующие проблемы, которые лучше всего сформулировать в терминах задачи выбора:

• либо априори предполагается, что все данные независимы, и использовать менее трудоемкие методы вычислений, за что придется платить снижением достоверности результатов;

• либо нужно организовать отслеживание зависимости между используемыми данными, количественно оценить эту зависимость, реализовать оперативное обновление соответствующей нормативной информации, т.е. усложнить вычисления, но получить более достоверные результаты.

Рассмотрим альтернативный подход, с помощью которого удается обойти указанные сложности при построении экспертных систем.