Для того, чтобы определить на основе выборочных данных равны ли дисперсии или нет, мы рассмотрим процедуру проверки гипотезы о равенстве дисперсий двух независимых нормально распределённых случайных величин. Эта задача имеет также самостоятельное значение, поскольку дисперсия характеризует точность работы приборов или технологических процессов, обработки данных и т.п. Убедившись в равенстве двух дисперсий, мы тем самым убеждаемся, например, в том, что два прибора обеспечивают одинаковую точность.
В математической статистике доказывается, что если гипотеза о равенстве дисперсий двух случайных величин выполняется: H0: 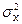 =
=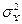 , то величина
, то величина  распределена в соответствии с законом распределения Фишера.
распределена в соответствии с законом распределения Фишера.
Это отношение F называют дисперсионным отношением Фишера и используют в качестве критерия проверки нулевой гипотезы.
Распределение Фишера характеризуется наличием степеней свободы, которые вычисляются по формулам:
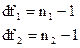
Поскольку величина F - неотрицательная, то критическая область данной величины будет принадлежать интервалу (0;+¥).
Альтернативными гипотезами являются гипотезы:
Н1: 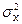 >
>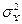 при
при 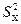 >
>
Н1: 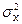 <
<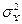 при
при 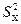 <
<
Последовательность проверки гипотезы:
1. Производится расчёт F -статистики Фишера.
2. Pадаёмся уровнем значимости 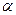 , который находится в пределах от 0,01 до 0,05.
, который находится в пределах от 0,01 до 0,05.
3. Вычисляется число степеней свободы: df1, df2.
4. Находим критическое значение Fкр равное F 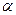 , df1,df2, используя таблицы, либо с помощью функции FРАСПОБР.
, df1,df2, используя таблицы, либо с помощью функции FРАСПОБР.
5. Сравниваем рассчитанное значение значения F- статистики и критическое: если F расч > Fкр, то гипотеза отвергается.
Инструмент анализа «двухвыборочный F- тест для дисперсий»
Служит для проверки нулевой гипотезы.
Последовательность действий:
- задаются интервалы Х и У;
- задаётся уровень значимости.
Выдаются:
- средние значения для случайной переменной Х и У,
- дисперсии для Х и У,
- число наблюдений,
- значение F -критерия,
- критическое значение.
Кроме инструмента анализа «двухвыборочный F- тест для дисперсий» можно использовать функции:
1. = ФТЕСТ (аналогичен режиму «двухвыборочный F- тест для дисперсий»).
2. = FРАСПОБР (для нахождения критического значения)).
3. = FРАСП (вычисляет p -уровень для расчетного значения F- статистики, и этот p -уровень сравнивается с уровнем значимости 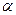 . Для того, чтобы принять гипотезу о равенстве дисперсий p - уровень должен быть больше уровня значимости
. Для того, чтобы принять гипотезу о равенстве дисперсий p - уровень должен быть больше уровня значимости 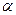 ).
).
 2014-02-02
2014-02-02 4300
4300
