Сравнение двух дисперсий

При обработке результатов наблюдений и измерений часто возникает необходимость сравнения выборочных дисперсий единичных значений двух выборок 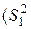и 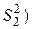с объемами соответственно n₁ и n₂. Основная статистическая гипотеза, которая при этом проверяется, – можно ли считать сравниваемые дисперсии равными друг другу (однородными). Если сравниваемые дисперсии однородны, то можно делать вывод о равенстве случайных ошибок в двух выборках или об одинаковой воспроизводимости измерений в них. Метод сравнения двух дисперсий используется для сопоставления случайных ошибок двух методов измерения, средств измерения, исследователей, лабораторий.

Рассмотрим две выборки а₁, а₂, а₃,...... а_i......, а_n1 и

b₁, b₂, b₃,......b_i,......, b_n2.

Выборочные дисперсии единичных значений для них рассчитываются по формулам:

;

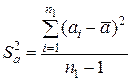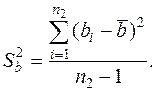
Данные дисперсии определяются со степенями свободы (f), которые являются знаменателями в формулах для расчета соответствующих дисперсий:

f_a = n₁ – 1 и f_b = n₂ -1.

Для статистической проверки равенства двух дисперсий выбирают максимальную (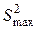) и минимальную (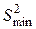) по величине дисперсию и рассчитывают F-соотношение (F_p) по следующей формуле:

.

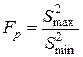Затем по распределению Фишера в зависимости от значений F_p, степеней свободы f_a и f_b рассчитывают соответствующую им доверительную вероятность (Р) вывода о равенстве дисперсий либо для заданной вероятности, например из табл. 5.3, определяют значение критерия Фишера (F_Т). При использовании табличной формы распределения Фишера в качестве f₁ используют степень свободы максимальной по величине дисперсии, а в качестве f₂ – степень свободы минимальной дисперсии.

Если рассчитанное значение F_p превосходит определенное F_Т (F_p > F_Т), то с доверительной вероятностью можно считать дисперсии различными (неоднородными). В противном случае (F_p ≤ F_Т) для заданной доверительной вероятности можно предположить, что дисперсии равны (однородны).

Пример [6]. Для изучения воспроизводимости работы рН-метра в кислой и щелочной областях проведены измерения рН в шести порциях буферного раствора I (х) и пяти порциях буферного раствора II (y) и получены следующие результаты:

Номер раствора	Значение рН раствора в порции
1	2	3	4	5	6
I	3,82	3,86	3,83	3,80	3,81	3,86
II	9,18	9,13	9,15	9,18	9,16

Можно ли считать случайные ошибки при работе рН-метра в кислой и щелочной средах одинаковыми?

Для ответа на этот вопрос рассчитаем выборочные дисперсии единичных значений рН для двух растворов:

;

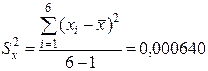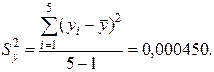
Составим F-отношение максимальной дисперсии к минимальной:

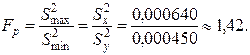
Из данных табл. 5.3 выбираем табличное значение квантиля распределения Фишера (F_Т) для f₁ = f_x = 6-1, f₂ = f_y = 5-1 и Р = 0,95. При вероятности 0,95 (соответствующий ей уровень значимости β = 1-Р = 1-0,95 = 0,05) для f₁ = 5 и f₂ =4 квантиль распределения Фишера имеет значение F_Т = 6,3. Так как F_Р < F_Т (0,142 < 6,3), то следует считать сравниваемые дисперсии равными, т.е. случайные ошибки одинаковыми при работе рН-метра в кислой и щелочной средах, а результаты измерений воспроизводимыми.

6.3. Сравнение нескольких дисперсий выборок
одинакового объема

Задача сравнения нескольких дисперсий наиболее часто возникает при оценке равенства случайных ошибок в нескольких опытах, у нескольких исследователей или лабораторий.

Пусть имеется n независимых нормально распределенных выборок с объемами m₁, m₂, m₃,...., mj,...., m_n и соответствующими им дисперсиями , , ,...., ,...., .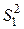

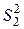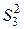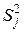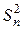Если объемы выборок одинаковы m₁ = m₂ = m₃ =....= m_j = m_n = m, то для сравнения дисперсий можно использовать критерий Кохрена G [5]. С этой целью сначала вычисляют расчетное значение G_p:

,

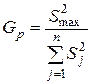где 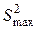- максимальная дисперсия.

Затем по распределению Кохрена в зависимости от значений G_p, числа сравниваемых дисперсий n и степени свободы f =m-1 рассчитывают соответствующую им доверительную вероятность (Р) вывода о равенстве дисперсий, либо для заданной вероятности и величины f, например из табл. 5.1, определяют значение критерия Кохрена (G_Т). Если рассчитанное значение G_p превосходит определенное G_Т (G_p > G_Т), то с доверительной вероятностью можно считать дисперсии различными (неоднородными). В противном случае (G_p ≤ G_Т) для заданной доверительной вероятности можно предположить, что дисперсии равны (однородны).

Пример. В задании 4 варианта 5 данных методических рекомендаций приведены результаты исследования влияния содержания пластификатора в резине на ее степень набухания. Влияет ли содержание пластификатора в резине на величину случайных ошибок измерения ее степени набухания?

Для ответа на этот вопрос рассчитаем выборочные дисперсии единичных значений степени набухания резины при различном содержании в ней пластификатора (для различных опытов с 1 по 5):

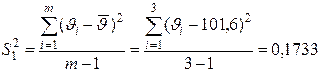(% мас.)²; 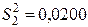(% мас.)²;

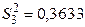(% мас.)²; 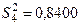(% мас.)²; 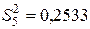(% мас.)².

Поскольку в каждом опыте проводилось одинаковое число повторных измерений степени набухания резины (m = 3), то для сравнения дисперсий можно воспользоваться критерием Кохрена.

Максимальной по величине дисперсией является дисперсия четвертого опыта. Рассчитаем значение Gp:

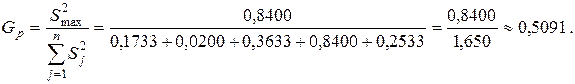
Для вероятности Р = 0,95 и величиныf =3-1 = 2 из табл. 5.1 определяем значение критерия Кохрена G_Т = 0,6838. Так как G_p < G_Т (0,5091 < 0,6838), то с вероятностью 0,95 можно считать, что все пять дисперсий равны друг другу (однородны). Исходя из этого вывода выборочная дисперсия единичных значений степени набухания резины всех опытов эксперимента (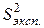) со степенью свободы f_эксп. = n(m-1) = 10 будет равна среднему арифметическому значению всех дисперсий [5,6]:

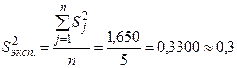(% мас.)²_.