Распределение Фишера

Важные приложения имеет в статистике св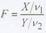

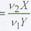
где X - случайная величина, распределенная по закону х² с v1 степенями свободы, а Y св, распределенная по закону х² с v2степенями свободы.

Случайная величина F распределена по закону, называемому законом распределения Фишера с v1степенями свободы. График плотности вероятностей распределения Фишера

При заданных числах v1 и v2и по вероятности а по таблице Фишера определяется значение F_α такое, что Р(F > F _а) =а. Обычно таблицы составляются для значений а, равных 0.05 или 0,01, а иногда для обоих этих значений.

Сходимость случайных величин. Неравенства Чебышева.

Сходимость случайных величин.

При изучении предельных теорем рассматриваются различные виды сходимости случайных величин. Наиболее часто употребляется понятие сходимости по вероятности.

Последовательность случайных величин {Х_п( 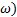} сходится к случайной величине Х( 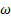) по вероятности

и обозначается 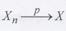, если для любого 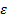> 0 выполняется равенство:

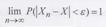
Следовательно, вероятность того, что Хn, отличается от X меньше любой заданной величины, близка к единице при достаточно больших п.

Теорема Чебышева.

Если случайная величина X имеет конечный первый абсолютный момент v1 = М(| Х |), то при любом
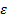> 0 выполняется неравенство

 

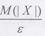
В частности, если X 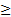0 и существует математическое ожидание М(Х), то справедливо первое неравенство

Чебышева: 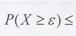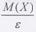и P(x<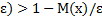

 

Для доказательства теорем, относящихся к закону больших чисел, используют второе неравенство Чебышева.

Второе неравенство Чебышева. Вероятность того, что величина X отклоняется от своего математического

ожидания не меньше любого положительного числа 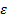, ограничена сверху величиной D(Х)/ 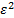, т.е.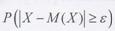

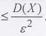
Иногда неравенство Чебышева записывают в виде

 

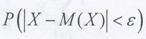
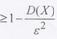
Теорема Чебышева.

Теорема Чебышева - одна из простейших, но наиболее важных форм закона больших чисел.

Рассмотрим случайную величину X, закон распределения которой от эксперимента к эксперименту изменяется, т.е. имеем дело с несколькими (n) случайными величинами.

Теорема Чебышева. Если Х1,Х2,...,Х_п.,... независимые случайные величины с конечными

математическими ожиданиями М(Хi), i= 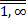, и дисперсиями D(Хi), i = 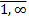ограниченными одним и тем же числом С, т.е. D(Х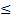i) С, i= 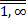, то при возрастании п среднее арифметическое наблюденных значений Xi, i= 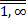, сходится по вероятности к среднему арифметическому их математических ожиданий, т.е. для любого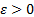

 

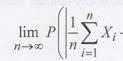
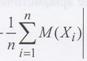
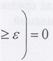(7.5)

Из теоремы следует, что среднее арифметическое достаточно большого числа независимых случайных величин (дисперсии которых равномерно ограничены) перестает быть случайной величиной, т.е. оно является

устойчивым и сходится по вероятности к определенной не случайной величине, т.к. среднее арифметическое

математических ожиданий 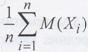- величина не случайная.

 

Если в формуле (7.5) перейти к вероятности противоположного события, получим другую формулировку закона больших чисел:

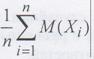
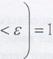
При доказательстве этого равенства с помощью второго неравенства Чебышева можно получить оценку:

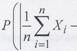
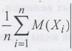
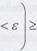
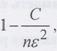
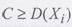
Частным случаем теоремы Чебышева для одинаково распределенных случайных величин Xi является теорема Хинчина.