Линейное дифференциальное уравнение теплопроводности для тел классической формы при отсутствии внутренних источников теплоты имеет вид
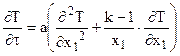 ,
,
где x1 – первая координата в ортогональной системе координат; k = 1, 2 или 3 – коэффициент формы тела; k – коэффициент температуропроводности.
Температурное поле будем находить в расчетной области, ограниченной осью симметрии тела и его внешней границей (см. рис. 1.2). Для выделения единственного решения данного уравнения зададим условия однозначности:
— размер расчетной области 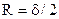 ;
;
— теплофизические свойства материала тела известны: a и λ;
— внутренние источники теплоты отсутствуют: 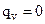 ;
;
— начальные условия: Т (х1, 0)=Т0;
— граничные условия:
а) на внутренней границе из условия симметрии температурного поля следует, что 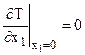 ;
;
б) на внешней границе теплообмен определяется температурой окружающей среды Tf и коэффициентом теплоотдачи 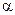
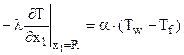 .
.
Решением поставленной задачи будет температурное поле  для заданных условий однозначности.
для заданных условий однозначности.
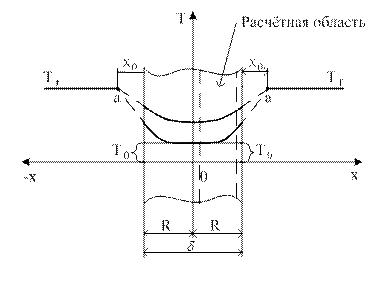
Рис. 2.2. К расчету температурного поля при ГУ III рода
В практике инженерных расчетов находят общее решение температурного поля в безразмерном виде  в зависимости от безразмерного коэффициента теплоотдачи – критерия Био (Bi) в безразмерных точках пространства (X) в моменты времени Fo. В этом случае математическая формулировка задачи имеет вид:
в зависимости от безразмерного коэффициента теплоотдачи – критерия Био (Bi) в безразмерных точках пространства (X) в моменты времени Fo. В этом случае математическая формулировка задачи имеет вид:
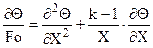 .
.
Начальное условие 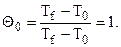
Граничные условия:
а) на внутренней границе 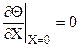 ;
;
б) на внешней границе 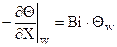 ,
,
где 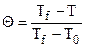 – безразмерная температура;
– безразмерная температура; 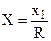 – безразмерная координата; R – характерный или определяющий размер тела;
– безразмерная координата; R – характерный или определяющий размер тела; 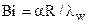 – критерий Биó; λw – коэффициент теплопроводности твердого тела;
– критерий Биó; λw – коэффициент теплопроводности твердого тела; 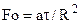 – безразмерное время – критерий Фурье.
– безразмерное время – критерий Фурье.
В результате решения задачи нестационарной теплопроводности, записанной в безразмерном виде, получаем функциональную зависимость  . Для удобства анализа решения данную зависимость представляют графически для теплового центра и поверхности каждого тела в отдельности. Т.о. наиболее часто используют шесть графиков зависимости
. Для удобства анализа решения данную зависимость представляют графически для теплового центра и поверхности каждого тела в отдельности. Т.о. наиболее часто используют шесть графиков зависимости 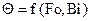 для конкретных значений k=1,2 и 3 в точках X=0 и X=1, которые приведены в учебниках по ТМО и в методических указаниях №1684. На рис. 2.3. показан общий вид номограммы расчета нестационарной теплопроводности в телах простейшей формы при граничных условиях III рода.
для конкретных значений k=1,2 и 3 в точках X=0 и X=1, которые приведены в учебниках по ТМО и в методических указаниях №1684. На рис. 2.3. показан общий вид номограммы расчета нестационарной теплопроводности в телах простейшей формы при граничных условиях III рода.
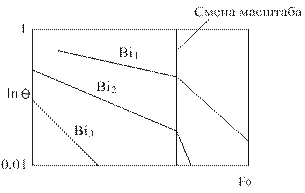
Рис.2.3. Номограмма для расчета нестационарной теплопроводности при ГУ III рода
При расчете нестационарной теплопроводности существует 2 основные постановки задачи: прямая и обратная. Целью решения прямой задачи является определение температурного поля (Θ) при заданных условиях однозначности (Fo, Bi). В результате решения обратной задачи теплопроводности по известному температурному полю (Θ) находят условия однозначности – время процесса теплопроводности или коэффициент теплоотдачи. Если по условию задачи заданы Θ и Bi, то по графику 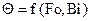 определяют критерий Fo, а затем время процесса. Если по условию задачи заданы Θ и Fo, то по графику
определяют критерий Fo, а затем время процесса. Если по условию задачи заданы Θ и Fo, то по графику 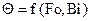 определяют критерий Bi, по значению которого рассчитывают коэффициент теплоотдачи.
определяют критерий Bi, по значению которого рассчитывают коэффициент теплоотдачи.
Прямая постановка задачи расчета нестационарной теплопроводности
Дано: 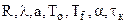 , где
, где 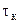 – время нагрева или охлаждения тела
– время нагрева или охлаждения тела
Найти: 1) температуру поверхности тела 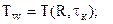
2) температуру теплового центра тела 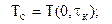
3) среднюю по массе температуру тела 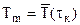 .
.
Алгоритм поставленной выше задачи заключается в следующем.
1. Перед началом расчета необходимо рассчитать размер расчетной области R, который для бесконечного цилиндра и шара равен радиусу тела, а для бесконечной пластины 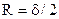 – при симметричном нагреве или охлаждении и, соответственно,
– при симметричном нагреве или охлаждении и, соответственно, 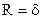 , если теплообмен на одной из сторон пластины отсутствует – несимметричный процесс теплопроводности.
, если теплообмен на одной из сторон пластины отсутствует – несимметричный процесс теплопроводности.
2. Рассчитываем критерии 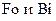 и по графикам для поверхности и теплового центра тела определяем безразмерные температуры поверхности
и по графикам для поверхности и теплового центра тела определяем безразмерные температуры поверхности 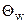 и центра
и центра 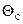 соответственно.
соответственно.

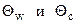
3. Находим температуры на поверхности и в центре тела. Т.к. по определению 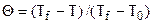 , то, выражая неизвестную температуру, получим
, то, выражая неизвестную температуру, получим 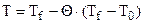 , где Т = Тw, если
, где Т = Тw, если 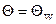 и Т = Тс, если
и Т = Тс, если 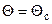 .
.
4) Рассчитываем среднюю по массе температуру тела в конце процесса теплопроводности. При допущении параболического распределения температуры по сечению тел простейшей формы формула для расчета среднемассовой температуры будет иметь вид:
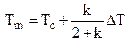 ,
,
где k – коэффициент формы тела; 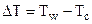 – перепад температур по сечению тела.
– перепад температур по сечению тела.
Обратная постановка задачи расчета нестационарной теплопроводности
А. Определение времени процесса нагрева/охлаждения
Дано: 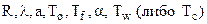
Найти: 1) время процесса теплопроводности – 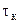 ;
;
2) температуру теплового центра 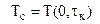 , либо температуру поверхности
, либо температуру поверхности 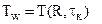 ;
;
3) среднюю по массе температуру тела 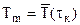 .
.
Алгоритм поставленной выше задачи заключается в следующем.
1. Перед началом расчета необходимо рассчитать размер расчетной области R, который для бесконечного цилиндра и шара равен радиусу тела, а для бесконечной пластины 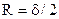 – при симметричном нагреве или охлаждении и, соответственно,
– при симметричном нагреве или охлаждении и, соответственно, 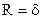 , если теплообмен на одной из сторон пластины отсутствует – несимметричный процесс теплопроводности.
, если теплообмен на одной из сторон пластины отсутствует – несимметричный процесс теплопроводности.
2. Рассчитываем температурные критерии 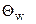 , либо
, либо 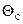 в зависимости от исходных данных и критерий Bi. Затем по графикам
в зависимости от исходных данных и критерий Bi. Затем по графикам 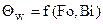 или
или 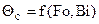 определяем критерий Фурье.
определяем критерий Фурье.
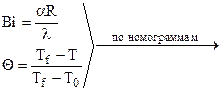
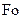
3. Рассчитываем время процесса по формуле 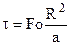 .
.
4. Неизвестную температуру и среднемассовую температуру находим по алгоритму решения прямой задачи.
Б. Определение коэффициента теплоотдачи от внешней среды к поверхности тела
Дано: 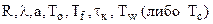
Найти: 1) коэффициент теплоотдачи – 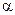 ;
;
2) температуру теплового центра 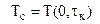 , либо температуру поверхности
, либо температуру поверхности 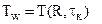 ;
;
3) среднюю по массе температуру тела 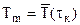 .
.
Алгоритм поставленной выше задачи заключается в следующем.
1. Перед началом расчета необходимо рассчитать размер расчетной области R, который для бесконечного цилиндра и шара равен радиусу тела, а для бесконечной пластины 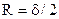 – при симметричном нагреве или охлаждении и, соответственно,
– при симметричном нагреве или охлаждении и, соответственно, 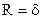 , если теплообмен на одной из сторон пластины отсутствует – несимметричный процесс теплопроводности.
, если теплообмен на одной из сторон пластины отсутствует – несимметричный процесс теплопроводности.
2. Рассчитываем температурные критерии 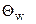 , либо
, либо 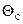 в зависимости от исходных данных и критерий Fo. Затем по графикам
в зависимости от исходных данных и критерий Fo. Затем по графикам 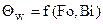 или
или 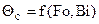 определяем критерий Био.
определяем критерий Био.
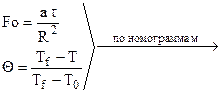

3. Рассчитываем коэффициент теплоотдачи по формуле 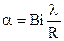 .
.
4. Неизвестную температуру и среднемассовую температуру находим по алгоритму решения прямой задачи.
 2014-02-02
2014-02-02 2997
2997
