Дифференциальное уравнение теплопроводности. (Дифференциальное уравнение Фурье)

(Дифференциальное уравнение Фурье)

Если поместить тело, например, бесконечную пластинку толщиной δ и начальной температурой T₀ в горячую среду с температурой T_f (рис. 1.1), то пластинка, получая энергию от горячей среды, будет нагреваться, и ее температура изменяется с течением времени в каждой точке.

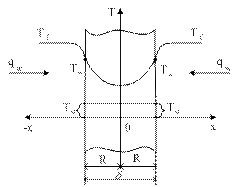
Рис. 2.1. Нагрев пластины в среде с температурой T_f

Температурное поле, т.е. распределение температур в пространстве и во времени, находят решением дифференциального уравнения (ДУ) теплопроводности, которое в 1814 году вывел французский ученый Фурье и поэтому это уравнение носит его имя. Вывод ДУ теплопроводности основан на законе сохранения энергии и использует закон Фурье. Уравнение Фурье моделирует процессы, которые в процессе теплопроводности протекают в каждом элементарном объеме тела:

1) поглощение тепловой энергии при нагреве или выделение при охлаждении;

2) прохождение теплоты через элементарный объем транзитом;

3) выделение или поглощение теплоты за счет действия внутренних источников или стоков теплоты мощностью q_v.

В векторной форме записи дифференциальное уравнение теплопроводности имеет вид:

,

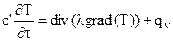где 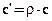– удельная объемная теплоемкость, Дж/(м³×К);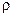– плотность, кг/м³; с – удельная массовая теплоемкость, Дж/(кг×К).

Напомним, что для твёрдых тел .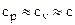

Решая это уравнение, мы получим температурное поле: Т(х_i, t). Т.о. дифференциальное уравнение теплопроводности устанавливает связь между пространственным и временным изменениями температуры.

Вид формул для операторов дивергенции (div) и градиента (grad) зависят от выбора системы координат. Например, в декартовой системе координат ДУ теплопроводности примет вид:

,

или принимая допущение о независимости физических свойств вещества от температуры {}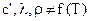

,

где 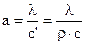– коэффициент температуропроводности, м²/с.

В нашем кратком курсе ТМО будем решать дифференциальное уравнение Фурье для тел простейшей формы (бесконечная пластина, бесконечный цилиндр и шар или сфера) с постоянными физическими коэффициентами:

,

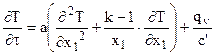где x₁ – первая координата в ортогональной системе координат: x₁ = x в декартовой системе координат, x₁ = r в цилиндрической и сферической системах координат; k = 1, 2 или 3 – коэффициент формы тела: k = 1 – бесконечная пластина; k = 2 – бесконечный цилиндр; k = 3 – шар.

При отсутствии в системе внутренних источников\стоков теплоты (q_v = 0) дифференциальные уравнения Фурье для тел простейшей формы записываются следующим образом:

k = 1: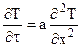; k = 2: 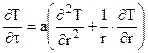;k = 3: .

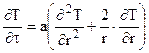При неизменных условиях теплообмена (постоянных температурах флюида, омывающих тело с разных сторон, и постоянных коэффициентах теплоотдачи) на границах тела его температурное поле с некоторого момента времени перестает изменяться во времени и наступает стационарный режим теплопроводности, который для тел простейшей формы описывается уравнением Пуассона при действии внутренних источников теплоты

,

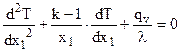или уравнением Лапласа, если q_v =0

.

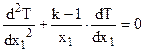В результате решения одномерного дифференциального уравнения для стационарного процесса теплопроводности находят температурное поле в виде T(x₁) или в явном виде T(x) – в декартовой системе координат и T(r) – в цилиндрической и сферической системах координат.

§4. Условия однозначности,