Транспортная задача в сетевой форме
Таблица 1.36
Таблица 1.35
Таблица 1.33
Таблица 1.32
Таблица 1.31
Таблица 1.25
Таблица 1.23
Таблица 1.19
Таблица 1.16
Таблица 1.15
Таблица 1.13
| Станции отправления | Запасы грузов | Станции назначения | |||
| B1 | B2 | B3 | B4 | ||
| A1 | 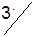
| 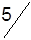
| 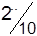
| 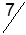
| |
| A2 | 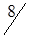
| 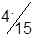
| 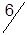
| 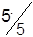
| |
| A3 | 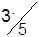
| 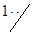
| 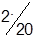
| 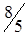
|
2. Проверим баланс наличия и потребления.
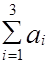 = 10 + 20 + 30 = 60;
= 10 + 20 + 30 = 60;
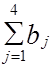 = 5 + 15 + 30 + 10 =60.
= 5 + 15 + 30 + 10 =60.
В нашем примере 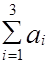 =
= 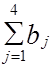 , т.е. общее количество грузов на станциях отправления равно суммарной потребности в этом грузе на всех станциях назначения.
, т.е. общее количество грузов на станциях отправления равно суммарной потребности в этом грузе на всех станциях назначения.
3. Методом двойного предпочтения найдем опорный план перевозок. На матрице стоимостей отмечены клетки и дан предварительный план перевозок, отвечающий условиям (1.26) - (1.28).
Проверим необходимое условие в опорном плане:
m=3; n=4; r=m+n-1=3+4-1=6.
Условие выполняется.
4. Выписываем матрицу стоимостей с табл. 1.13.
В табл. 1.14 отмечаем кружочками загруженные клетки, т.е. маршруты перевозок.
Таблица 1.14
| (2) | ||||
 8 8
| (4) | ||||
| (8) |
|
 Справа от матрицы стоимостей записываем значение потенциалов Ui, а под нижней строкой матрицы стоимостей - потенциалы Vj. Эти потенциалы можно получить следующим образом. Положим, чтобы потенциалы выровняли до нуля тарифы во всех загруженных клетках, т.е.
Справа от матрицы стоимостей записываем значение потенциалов Ui, а под нижней строкой матрицы стоимостей - потенциалы Vj. Эти потенциалы можно получить следующим образом. Положим, чтобы потенциалы выровняли до нуля тарифы во всех загруженных клетках, т.е.
 2 + U1 + V3 = 0;
2 + U1 + V3 = 0;
4 + U2 + V2 = 0;
5 + U2 + V1 = 0; (1.40)
3 + U3 + V1 = 0;
2 + U3 + V3 = 0;
8 + U3 + V4 = 0.
Дадим первой неизвестной произвольное значение, например U1=0.
Тогда все другие неизвестные определяются из составленной системы (1.40): V3= - 2; U3 = 0; V4 = - 8; U2 = 3; V2 = - 7; V4 = - 3.
В табл. 1.15 показана преобразованная матрица стоимостей.
Каждый элемент ее представляет собой алгебраическую сумму трех слагаемых одноименного элемента предыдущей матрицы (табл. 1.14) и соответствующих потенциалов Ui и Vj. Все отмеченные (загруженные) элементы преобразованной матрицы стоимостей равны нулю.
5. Однако предварительный план перевозок, образующий матрицу стоимостей в табл. 1.15, не является оптимальным, т.к. есть элементы со стоимостью Cij<0. В этой ситуации необходима корректировка плана или перераспределение грузопотока. Для этого выберем максимальную по модулю отрицательную стоимость
Cij=-max[Cij].
| C11 | C12 | - 2 | C13 | (0) | - 1 | C14 | |||||

| C22 | (0) | C23 | (0) | C24 | ||||||
| (0) | C32 | - 6 | C33 | (0) | (0) | C34 |
В нашем случае это элемент C32= - 6. Далее, используя этот элемент и другие загруженные элементы преобразованной матрицы стоимости, строим цикл и, начиная с отрицательного элемента C32, нумеруем вершины цикла римскими цифрами, двигаясь по часовой стрелке.
6. В четных клетках (2,2) и (3,4) имеются грузопотоки соответственно 15 и 5 единиц.
7. Из всех маршрутов, приходящихся на вершины цикла с четными номерами, выбираем маршрут с минимальной перевозкой. В нашем примере Х34=5. Эту поставку переносим из всех четных загруженных клеток в нечетные, т.е. объем этой перевозки вычтем из всех объемов перевозок, приходящихся на четные номера цикла, и прибавим к объемам перевозок, приходящихся на нечетные номера.
При этом одна клетка (3,4) разгрузилась, а другая (3,2) нагрузилась. Получился новый план (табл. 1.16.), который, в свою очередь, следует проверить на отрицательность.
| Станции отправления | Запасы грузов | Станции назначения | |||
| B1 | B2 | B3 | B4 | ||
| A1 | 
| 
| 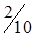
| 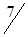
| |
| A2 | 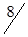
| 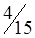
| 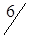
| 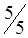
| |
| A3 | 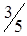
| 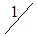
| 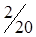
| 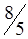
|
Выписываем матрицу стоимостей (табл. 1.17) и в соответствии с новым планом назначений отмечаем загруженные клетки.
В табл. 1.17 полагаем, чтобы потенциалы выровняли до нуля тарифы во всех отмеченных клетках, т.е.
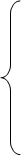 2 + U1 + V3 = 0;
2 + U1 + V3 = 0;
4 + U2 + V2 = 0;
5 + U2 + V1 = 0; (1.41)
3 + U3 + V1 = 0;
2 + U3 + V3 = 0;
8 + U3 + V4 = 0.
Для этого придаем первой неизвестной произвольное значение, скажем, U1=0, тогда остальные неизвестные примут следующие значения:
U1= 0; U2= - 3; U3= 0; U4= -2; V1= -3; V2= - 1; V3= - 2; V4= - 4
Таблица 1.17
- 3
| (2) | |||
| (4) | (5) | ||
| (3) | (1) | (2) |
|
Справа от матрицы стоимостей (табл. 1.17) записываем значение потенциалов Ui, а под нижней строкой - потенциалы Vj.
В табл. 1.18 показана вновь преобразованная матрица стоимостей.
Таблица 1.18
В табл. 1.18 не оказалось отрицательных тарифов, следовательно, выполняется условие Ui+Vj+Cij>=0 и план перевозок является оптимальным. Итак, задача имеет оптимальное значение, если грузопотоки будут:
Х13=10; X22=10; X24=10; X31=5; X32=5; X33=20.
При этом
F=С13X13+C22X22+C24X24+C31X31+C32X32+C33X33+C33X33= =2*10+4*10+5*10+3*5+1*5+2*20=170 ед.
Первоначальные транспортные расходы F* составили:
F*=С13X13+С22X22+С24X24+С31X31+C33X33+C34X34= =2*10+4*15+5*5+3*5+2*20+8*5=200 ед.
Следовательно, оптимальный план F перевозок меньше по транспортным расходам первоначального плана перевозок F* на 30 ед.
Пример. При капитальном ремонте четырех путей в приемно-отправном парке станции используется щебень из трех карьеров. Запасы щебня в каждом из карьеров соответственно равны 120, 180 и 160 усл. ед. Потребности в щебне для каждого пути соответственно равны 130, 220, 60 и 70 усл. ед. Заданы тарифы перевозок 1 ед. щебня из каждого карьера и каждому из ремонтируемых путей:
С= 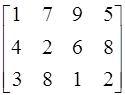 .
.
Составить такой план перевозок щебня, при котором потребности в нем каждого ремонтируемого пути были бы удовлетворены при наименьшей общей стоимости перевозок.
Решение
1. Исходные данные сведем в табл. 1.19.
| Станции отправления | Запасы грузов | Станции назначения | |||
| B1 | B2 | B3 | B4 | ||
| A1 | 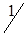
| 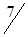
| 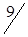
| 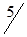
| |
| A2 | 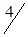
| 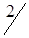
| 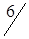
| 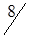
| |
| A3 | 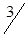
| 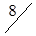
| 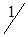
| 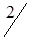
|
В табл. 1.19 через Аi (i=1,3) обозначены ремонтируемые пути, Bj (j=1,4) - карьеры.
2. Проверим баланс наличия и потребления:
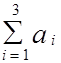 = 120 + 280 + 160 = 560 ед.
= 120 + 280 + 160 = 560 ед.
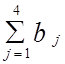 = 130 + 220 + 60 + 70 = 480 ед.
= 130 + 220 + 60 + 70 = 480 ед.
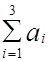
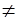
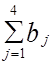 .
.
Запасы щебня в карьере больше, чем потребности в нем на ремонтируемых путях. Следовательно, модель исходной ТЗ является открытой. Чтобы получить закрытую модель, введем дополнительную станцию назначения В5 с потребностями, равными 560 - 480 = 80 усл. ед. Тарифы на перевозку единицы щебня из всех карьеров на станцию В5 полагаем равным нулю. В результате получаем закрытую модель ТЗ (табл. 1.20).
3. Методом двойного предпочтения построим предварительный план перевозок (табл. 1.20). Число перевозок r = m + n - 1 = 3 + 5 - 1 = 7. Условие соблюдается.
Таблица 1.20
| Станции отправления | Запасы грузов | Станции назначения | ||||
| B1 | B2 | B3 | B4 | B5 | ||
| A1 | 1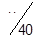
| 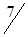
| 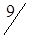
| 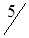
| 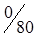
| |
| A2 | 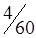
| 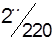
| 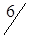
| 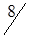
| 
| |
| A3 | 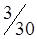
| 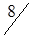
| 1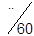
| 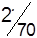
| 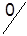
|
4. Проверим полученный план перевозок на отрицательность. Для чего выпишем матрицу стоимостей (табл. 1.21) и подберем потенциалы строк Ui и столбцов Vj так, чтобы выполнялись условия (1.37) и (1.38).
Таблица 1.21
| (0) | |||||
| (4) | (2) | (6) | (0) | |||
| (1) | (2) |
В табл. 1.21 потребуем, чтобы потенциалы выровняли до нуля тарифы во всех отмеченных клетках, т.е.
 1 + U1 + V1 = 0;
1 + U1 + V1 = 0;
0 + U1 + V5 = 0;
4 + U2 + V1 = 0;
3 + U3 + V1 = 0; (1.42)
2 + U2 + V2 = 0;
1 + U3 + V3 = 0;
2 + U4 + V4 = 0.
Пусть U1 = 0, тогда из полученной системы 1.42 находим:
U1 = 0; U2 = -3; U3 = -2; V1 = - 1; V2 = 1; V3 = 1; V4 = 0; V5 = 0.
Справа от матрицы стоимостей (табл. 1.21) записываем значение потенциалов Ui, а под нижней строкой - потенциалы Vj.
В табл. 1.22 показана вновь преобразованная матрица стоимостей.
Таблица 1.22
 (0) (0)
| (0) | |||||||
| - 3 | |||||||
| (0) | (0) | (0) | - 2 |
5. Полученный план перевозок, образующий матрицу стоимостей в табл. 1.22, не является оптимальным: C35 = -2; C25 = -3. Проведем корректировку плана. По выше изложенной методике строим цикл (табл. 1.22) и производим перераспределение грузопотока. Минимальная по объему перевозка находится у вершины II или в клетке (2,1) и равна 60 усл. ед. Перераспределяем перевозки. При этом клетка (3,1) разгрузилась, а другая клетка (2,5) нагрузилась. Получаем новый план перевозок (табл. 1.23).
Полученный план следует проверить на оптимальность, используя метод потенциалов.
| Станции отправления | Запасы грузов | Станции назначения | ||||
| B1 | B2 | B3 | B4 | B5 | ||
| A1 | 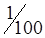
| 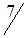
| 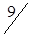
| 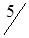
| 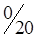
| |
| A2 | 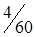
| 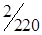
| 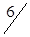
| 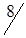
| 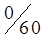
| |
| A3 | 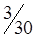
| 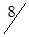
| 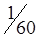
| 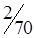
| 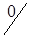
|
Выписываем матрицу стоимостей (табл. 1.24).
Таблица 1.24
- 2
| (1) | (0) | |||
| (2) | (0) | |||
| (3) | (1) | (20 |
|
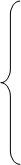 |
1 + U1 + V1 = 0;
0 + U1 + V5 = 0;
2 + U2 + V2 = 0;
0 + U2 + V5 = 0; (1.43)
3 + U3 + V1 = 0;
1 + U3 + V3 = 0;
2 + U3 + V4 = 0.
Пусть U1=0, тогда из (1.43) находим:
V1 = - 1; V5 = 0; U2 = 0; V2 = - 2; V3 = 1; U3 = 1; V4 = 0.
Преобразованная матрица показана в табл. 1.25

| (0) | |||||||
| (0) | (0) | |||||||
| (0) | (0) | - 2 |
6. Полученный план неоптимальный, поскольку С35 = -2 < 0. Строим цикл по выше приведенным правилам и производим корректировку плана перевозок. При этом клетка (1,5) разгрузилась, а клетка (3,5) нагрузилась. Новый план перевозок представлен в табл. 1.26.
Таблица 1.26
| Станции отправления | Запасы грузов | Станции назначения | ||||
| B1 | B2 | B3 | B4 | B5 | ||
| A1 | 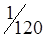
| 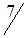
| 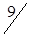
| 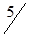
| 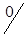
| |
| A2 | 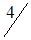
| 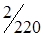
| 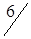
| 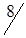
| 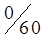
| |
| A3 | 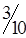
| 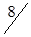
| 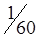
| 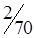
| 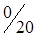
|
7. Полученный план перевозок проверим на отрицательность по вышеприведенной методике. Матрица стоимостей для нового приближения приведена в табл. 1.27.
|
| (1) | ||||||
| (2) | (0) | |||||
| (1) | (2) | (0) |
Подсчитаем потенциалы:
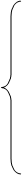 1 + U1 + V1 = 0;
1 + U1 + V1 = 0;
2 + U2 + V2 = 0;
0 + U2 + V5 = 0;
3 + U3 + V1 = 0; (1.44)
1 + U3 + V3 = 0;
2 + U3 + V4 = 0;
0 + U3 + V5 = 0.
Полагаем U1 = 0 и из полученной системы (1.44) находим:
V1 = - 1; V2 = 0; U2= - 2; V3 = 1; V4 = 0; V5 = 2.
Преобразованная матрица стоимостей приведена в табл. 1.28.
Таблица 1.28
Анализ табл. 1.28 показывает, что план перевозок является оптимальным и ТЗ имеет следующий оптимальный план:
X = 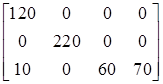 .
.
При этом плане остаются неиспользованными 60 усл. ед. щебня во втором карьере и 20 усл. ед. в третьем карьере. Общая стоимость перевозок составляет:
F = 1·120 + 3·10 + 2·220 + 1·60 + 2·70 = 790.
При первоначальном плане перевозок транспортные издержки составляют: F = 1·40 + 4·60 + 2·220 + 3·30 + 1·60 + 2·70 = 1010.
Оптимальный план перевозок на 220 ед. дешевле.
Пример. Составить оптимальный план перевозок для следующей ТЗ (табл. 1.29).
Решение.
1. Проверим баланс наличия и потребления:
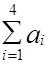 = 5 + 10 + 6 + 4 = 25;
= 5 + 10 + 6 + 4 = 25;
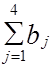 = 7 + 3 + 7 + 8 = 25;
= 7 + 3 + 7 + 8 = 25;
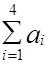 =
= 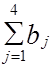 .
.
Задача сбалансированная.
Таблица 1.29
| Станции отправления | Запасы грузов | Станции назначения | |||
| B1 | B2 | B3 | B4 | ||
| A1 | 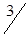
| 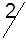
| 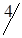
| 1 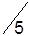
| |
| A2 | 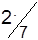
| 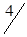
| 3. | 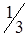
| |
| A3 | 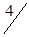
| 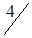
| 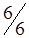
| 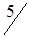
| |
| А4 | 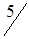
| 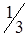
| 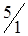
| 
|
Построенный цикл состоит из шести вершин и начинается от элемента с максимальной по модулю отрицательной величиной стоимости (клетка (2, 3)).
2. Методом двойного предпочтения определим предварительный план перевозок, отвечающий условиям (1.26) - (1.28).
Необходимое число перевозок r = m + n - 1 = 4 + 4 - 1 = 7.
Условия оптимального числа перевозок не выполняется, поэтому введем фиктивную перевозку x ij = 0. Она должна располагаться так, чтобы выполнялось условие (1.26). В табл. 1.29, в клетке (1, 2) квадратом отмечена фиктивная перевозка.
3. Из заданной таблицей ТЗ выписываем матрицу стоимости (табл. 1.30) и отмечаем те клетки, в которых есть перевозки.
 3 3
| (1) | ||
| (2) | (1) | ||
| (6) | |||
| (1) | (5) |
|
Справа от матрицы стоимости записываем значение потенциалов Ui. Следуя вышеизложенному правилу, имеем:
 2 + V2 + U1 = 0;
2 + V2 + U1 = 0;
1 + V4 + U1 = 0;
2 + V1 + U2 = 0;
1 + V4 + U2 = 0; (1.45)
6 + V3 + U3 = 0;
1 + V2 + U4 = 0;
5 + V3 + U4 = 0.
Полагая U1 = 0, тогда из (1.45) находим:
V2 = - 2; V4 = - 1; V1 = - 2; V3 = 6; U2 = 0; U3 = 0; U4 = 1.
В табл. 1.31 показана преобразованная матрица стоимости.
Поскольку табл. 1.31 содержит Cij < 0 клетка (2, 3) предварительный план перевозок не является оптимальным. В этой ситуации необходима корректировка плана перевозок, по вышеизложенному алгоритму строим цикл (табл. 1.31)
  1 1
| - 2 | (0) | |||||
| - 3 | (0) | |||||
| (0) | |||||||
| (0) | (0) |
Минимальная по объему перевозка находится у вершины IV цикла, клетка (1, 2).
Эта фиктивная перевозка, ее объем равен нулю. Во всех остальных отмеченных клетках имеются действительные перевозки за исключением клетки (2, 3), куда по правилам следует передвинуть фиктивную перевозку. Все остальные перевозки останутся без изменений, так как их объем изменяется на фиктивную величину, т.е. на ноль.
В табл. 1.32 показана матрица стоимости нового плана перевозок.
| (1) | ||||
 (2) (2)
| (1) | ||||
| (6) | |||||
| (1) | (5) |
Подсчитаем потенциалы.
 1 + V4 + U1 = 0;
1 + V4 + U1 = 0;
2 + V1 + U2 = 0;
3 + V3 + U2 = 0;
1 + V4 + U2 = 0; (1.46)
6 + V3 + U3 = 0;
1 + V2 + U4 = 0;
5 + V3 + U4 = 0.
Полагая U1 = 0, тогда из (1.46) находим:
V2 = 1; V4 = - 1; V1 = - 2; V3 = - 3; U2 = 0; U3 = - 3; U4 = - 2.
В табл. 1.33 показана преобразованная матрица тарифов.
Наличие отрицательного элемента, клетка (3, 1), в матрице дает основание утверждать, что новый план не является оптимальным, поэтому для перераспределения грузопотока строим цикл (табл. 1.33).
| (0) | |||||||
  (0) (0)
| (0) | ||||||
| (0) | ||||||
| (0) | (0) |
По вышеизложенному алгоритму, перераспределяем объемы перевозок (табл. 1.34).
Таблица 1.34
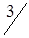
| 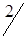
| 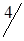
| 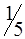
| |
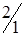
| 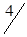
| 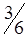
| 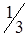
| |
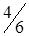
| 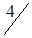
| 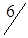
| 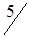
| |
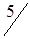
| 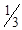
| 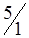
| 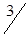
|
Проверим полученный план перевозок на оптимальность. Для этого выпишем матрицу тарифов (табл. 1.35) и отметим те клетки, в которых есть перевозки.
| (1) | ||||
| (2) | (3) | (1) | |||
| (4) | |||||
| (1) | (5) |
|
Найдем потенциалы Ui и Vj .
 1 + V4 + U1 = 0;
1 + V4 + U1 = 0;
2 + V1 + U2 = 0;
5 + V3 + U2 = 0;
1 + V4 + U2 = 0; (1.47)
4 + V1 + U3 = 0;
1 + V2 + U4 = 0;
5 + V3 + U4 = 0.
Пусть U1 = 0. Тогда из (1.47) находим:
V1 = - 2; V2 = 1; V3 = - 3; V4 = - 1;U2 = 0; U3 = - 2; U4 = - 2.
Преобразованная матрица тарифов показана в табл. 1.36.
Поскольку в табл. 1.36 нет отрицательных элементов, то полученный план перевозок оптимальный.
Для того чтобы окончательно убедиться в оптимальности плана перевозок, следует сравнить суммарные стоимости перевозок предварительного и оптимального планов, пользуясь целевой функцией F.
Общая стоимость перевозок по предварительному плану составит (табл. 1.29):
F' = 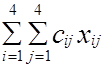 = 5 + 2 ·7 +3 + 6 ·6 + 3 + 5 = 66.
= 5 + 2 ·7 +3 + 6 ·6 + 3 + 5 = 66.
Для оптимального плана (табл. 1.34):
Fопт = 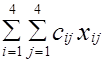 = 5 + 2 +3 ·6 + 3 + 4 ·6 + 5+3 = 60.
= 5 + 2 +3 ·6 + 3 + 4 ·6 + 5+3 = 60.
План в табл. 1.34 на шесть единиц дешевле предварительного плана (табл. 1.29).
В больших задачах по планированию перевозок массовых грузов решение ТЗ связано с большими трудностями, так как если количество станций отправления будет порядка несколько сотен, а количество станций назначения - тысячи, то соответствующая матрица тарифов будет содержать сотни тысяч элементов. Подготовка, хранение и преобразование в процессе вычислений столь обширной исходной информации - задача сложная, а порой и непреодолимая. В этом случае удобнее пользоваться ТЗ в сетевой форме. Дело в том, что реальные перевозки массовых грузов осуществляются по транспортным сетям, состоящим из участков, связывающих различные станции. Среди этих станций имеются станции отправления, назначения и участковые станции, через которые груз идет транзитом. Исходной информацией для расчета суммарных затрат на перевозки являются данные о затратах на перевозку единицы груза по каждому участку сети, количество которых лишь немногим отличается от количества связываемых станций. Следовательно, при тех же сотнях станций отправления и порядка тысячи станций назначения исходная информация будет содержать лишь две - три тысячи величин.
Положим, что имеющиеся станции отправления и назначения расположены на некоторой транспортной сети, состоящей из q участков связывающих между собой p станций. При этом нам удобно будет указанную сеть считать ориентированной. Это означает, что для дорог с двухпутным движением наряду с каждым участком at связывающим станцию it со станцией jt, придется вводить еще участок 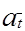 , связывающий станцию
, связывающий станцию 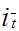 = jt со станцией
= jt со станцией 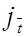 = it.
= it.
Таким образом, транспортная сеть будет задана некоторым ориентированным графом
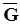 = (NA), где N =
= (NA), где N = 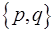 , A =
, A = 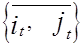 . (1.48)
. (1.48)
Граф - основное понятие теории графов, математически определяется как совокупность двух множеств - множества элементов V и множе-
ства отношений между этими элементами E, обозначается G = (V, E).
Геометрически удобно изображать граф в виде схемы - тогда элементы множества V будут точками (их называют вершинами V), а отношения E - отрезками, соединяющими элемент Vi с элементами, которые с ним связаны.

 Граф называется ориентированным (орграфом G = (V, E)), если всякая пара точек Vi, Vj упорядочена, т. е. соединяющее их ребро имеет начало и конец, тогда оно называется дугой. Каждой вершине i = 1, p орграфа G сопоставляется вещественное число b i. Если b i > 0, то это означает, что вершина i отвечает пункту производства, в котором объем производства равен b i. Если b i < 0, то соответствующая величина отвечает станции назначения с объемом потребления
Граф называется ориентированным (орграфом G = (V, E)), если всякая пара точек Vi, Vj упорядочена, т. е. соединяющее их ребро имеет начало и конец, тогда оно называется дугой. Каждой вершине i = 1, p орграфа G сопоставляется вещественное число b i. Если b i > 0, то это означает, что вершина i отвечает пункту производства, в котором объем производства равен b i. Если b i < 0, то соответствующая величина отвечает станции назначения с объемом потребления 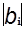 . Наконец, если b i = 0, то это участковая станция, которую груз проходит транзитом. При этом будем полагать, что задача сбалансированная. План перевозок определяется выбором q - мерного вектора
. Наконец, если b i = 0, то это участковая станция, которую груз проходит транзитом. При этом будем полагать, что задача сбалансированная. План перевозок определяется выбором q - мерного вектора
X = (x1, x2,..., xq); (1.49)
"x ³ 0
с неотрицательными элементами, указывающими планируемые объемы перевозок по всем участкам сети.
 Для каждой вершины i = 1, p орграфа G через
Для каждой вершины i = 1, p орграфа G через 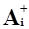 обозначим множество тех дуг, для которых jt = i, а через
обозначим множество тех дуг, для которых jt = i, а через 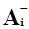 - множество тех дуг, для которых it = i.
- множество тех дуг, для которых it = i.
Тогда при фиксированном плане перевозок (1.49) количество ввозимого и вывозимого груза в каждую станцию может быть определено по формуле
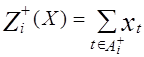 ;
; 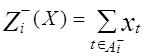 ; i =
; i = 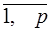 . (1.50)
. (1.50)
Это означает, что план перевозок (1.49) является допустимым, если он удовлетворяет условиям:
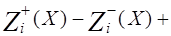 b i = 0, i =
b i = 0, i = 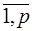 ; (1.51)
; (1.51)
или
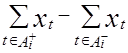 + b i = 0, i =
+ b i = 0, i = 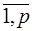 . (1.52)
. (1.52)
Если 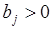 , то это означает, что вершина i отвечает пункту производства, в котором объем производства равен
, то это означает, что вершина i отвечает пункту производства, в котором объем производства равен 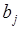 .
.
 Далее, каждой дуге a t, t = 1, q орграфа сопоставляется величина
Далее, каждой дуге a t, t = 1, q орграфа сопоставляется величина 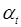 , указывающая затраты (тарифы), связанные с перевозкой единицы груза со станции it на станцию jt по соответствующему участку сети.
, указывающая затраты (тарифы), связанные с перевозкой единицы груза со станции it на станцию jt по соответствующему участку сети.
 Если
Если 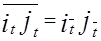 , то α t ¹ α t.
, то α t ¹ α t.
Задача состоит в нахождении такого допустимого плана перевозок (1.49), для которого достигается минимум суммарных транспортных издержек:
F = 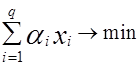 . (1.53)
. (1.53)

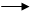 Таким образом, ТЗ в сетевой постановке можно сформулировать так: для фиксированного орграфа G при заданных величинах
Таким образом, ТЗ в сетевой постановке можно сформулировать так: для фиксированного орграфа G при заданных величинах 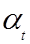 , b i, t = 1, q;
, b i, t = 1, q;
i = 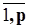 , удовлетворяющих условию баланса
, удовлетворяющих условию баланса
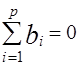 ,
,
определить q- мерный вектор (1.49), минимизирующий линейную функцию F = 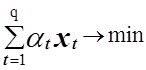 , при ограничениях (1.52).
, при ограничениях (1.52).
Рассмотрим решение ТЗ в сетевой форме [6].
Пример. Требуется построить оптимальный план перевозки груза на сети от трех станций отправления до девяти станций назначения.
Станции отправления груза обозначим квадратами, а станции назначения - кружочками. Цифрами между станциями указано расстояние перевозки, а в знаменателе для звеньев 1-7, 1-11, 2-9, 3-10 заданы ограничения пропускной способности (рис. 1.11).
Решение.
ТЗ в сетевой форме начинают решать с составления начального плана, который не допускает встречных перевозок на участках заданного полигона. Начальный (или любой допустимый) план характеризуется определенным числом базисных звеньев: K = n - 1, где n - число вершин, вошедших в полигон сети.
Для полигона (рис. 1.11) число базисных звеньев равно:
K = 13 - 1 = 12.
Звенья с потоком, равным пропускной способности, являются небазисными. Эти потоки называют перенасыщенными. Изображать их будем пунктирной стрелкой.
При решении задачи может встретиться случай вырождения, когда число базисных звеньев заданного полигона меньше числа K. В этом случае по свободному звену (желательно по звену с наименьшим расстоянием) пропускают нулевой поток и это звено в последующих операциях принимают за базисное. Базисным может стать и звено с потоком, равным пропускной способности.
В ходе решения возможен и такой случай, когда число базисных звеньев в допустимом плане больше числа K, например, если на сети получился замкнутый контур. Это означает, что допущена ошибка, которую необходимо устранить до построения системы потенциалов. Для избежания данного случая рекомендуется снабжать потребителей только от одного поставщика, а от двух, когда у первого не хватит ресурсов.
|

Возможный начальный план приведен в качестве примера на рис. 1.12, на котором знаком "+" отмечена вершина отправления груза, знаком "-" - вершина потребления (прибытия) на станции выгрузки, "- 40" - величина прибытия и "+ 200" - величина отправления груза. Поток на участке обозначен стрелкой в правопутном направлении, а величина грузопотока - числом у стрелки.
После построения начального (допустимого) плана, пример которого приведен на рис. 1.12, начинают строить на сети оптимальный план перевозок методом потенциалов. Любой допустимый план называют оптимальным тогда, когда вершине полигона могут быть присвоены некоторые числа (потенциалы) U и V, которые отвечают следующим условиям:
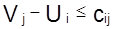 ; для x ij = 0, (1.54)
; для x ij = 0, (1.54)
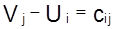 ; для 0 < x < dij, (1.55)
; для 0 < x < dij, (1.55)
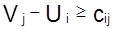 ; для x = dij, (1.56)
; для x = dij, (1.56)
где i, j - номера вершин полигона;
Ui, Vj - потенциалы соответственно i - й и j - й вершин;
Cij - расстояние от i - й до смежной j - й вершины (длина участка, соединяющего соседние станции);
x ij - грузопоток на звене ij;
dij - ограничение пропускной способности на участке ij.
|
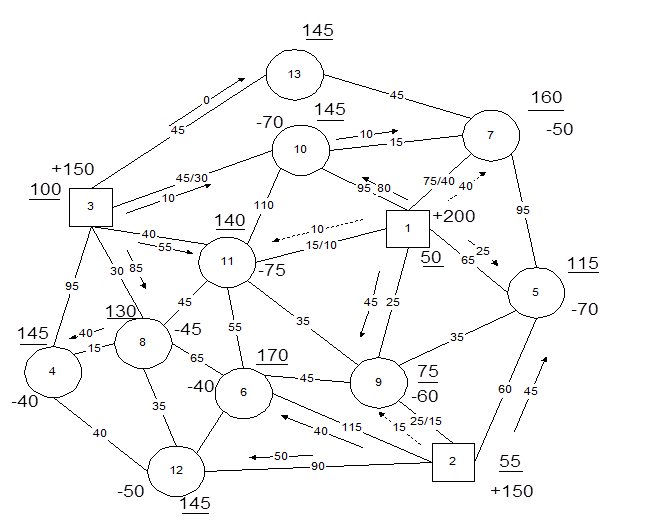
Для всех вершин полигона находят систему потенциалов. Какой-либо станции отправления присваивается начальный потенциал, например V3 = 100. Затем по базисным звеньям определяют потенциалы смежных вершин. Из условия оптимальности (1.49) следует, что
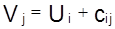 , (1.57)
, (1.57)
если известен потенциал вершины i, а по звену походит грузопоток в направлении от i к j. Например, V8 = U3 + C3.8 = 100 + 30 = 130.
Из этого же условия оптимальности следует, что
Ui = Vj + cij, (1.58)
если известен потенциал вершины j, а по звену проходит грузопоток в направлении от i к j. Например, U2 = V5 - C5.2 = 115 - 60 = 55.
Потенциалы всех вершин заданного полигона на рис. 1.12 подчеркнуты.
После построения системы потенциалов находят звенья сети с нарушением оптимальности (1.54) и (1.56) по формуле
Hij = Vj - Ui - cij. (1.59)
Для рассматриваемого примера имеются следующие нарушения условий оптимальности на свободных звеньях:
H5.9 = 115 - 75 - 35 =5,
H6.9 = 170 - 75 - 45 = 50.
Нарушения на звеньях с потоком, равным пропускной способности, отрицательны по своей величине:
H2.9 = 75 - 55 - 25 = -5.
Из всех звеньев с нарушениями выбирают звено, имеющее максимальную по модулю величину нарушения. Для этого звена строят замкнутый контур, состоящий из базисных звеньев и выбранного звена с нарушением. Если замкнутый контур состоит из попутных звеньев без ограничения пропускной способности, то на звено с нарушением назначают поток улучшения плана
x ул = min x ij встр. (1.60)
На величину потока улучшения плана X ул изменяют все потоки рассматриваемого контура: уменьшают встречные и увеличивают попутные потоки. Встречные и попутные потоки контура улучшенного плана находятся после определения направления следования потока на звене с нарушением. На рассматриваемом звене с нарушением, направления всегда будут от вершины с меньшим потенциалом, ограничивающей данное звено, к вершине с большим потенциалом, ограничивающей это звено с другой стороны. В направлении следования нового потока на свободном звене с нарушением просматриваются все потоки и из них находят попутные и встречные.
Если в замкнутом контуре есть попутные звенья с ограничением пропускной способности, то на звено с нарушением назначают поток
x ул = min 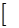 x ij встр, (dij - x ij)попутн
x ij встр, (dij - x ij)попутн . (1.61)
. (1.61)
Если звено с нарушением является перенасыщенным, то
x ул = min 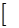 x ij попутн, (dij - x ij)встр
x ij попутн, (dij - x ij)встр . (1.62)
. (1.62)
В контуре попутные потоки уменьшают, встречные - увеличивают.
Следует помнить, что контур улучшения плана всегда может быть только один для рассматриваемого звена с нарушением.
После этого пересматриваются потенциалы вершин, входящих в рассмотренный контур, и смежных с ним вершин.
Улучшенная схема вновь проверяется на оптимальность. Если небазисные звенья удовлетворяют условиям (1.54) и (1.56), то получен оптимальный план. Если небазисные звенья этому условию не удовлетворяют, то решение продолжают.
На рис. 1.13 приведен один из вариантов оптимального плана.
По формуле (1.59) были рассчитаны разности для перенасыщенных звеньев:
H1.7 = 160 - 50 - 75 = +35;
H1.11 = 140 - 50 - 15 = +75;
H2.8 = 75 - 5 - 15 = +55.
Положительные разности на перенасыщенных звеньях говорят о перерасходе затрат. Недостаток пропускной способности звена I - II вызывает наибольший перерасход затрат, следовательно, увеличивать ее необходимо в первую очередь на этом звене.
Если бы было возможно увеличить пропускную способность d1.11, то экономия от этого равнялась 75 ед. стоимости на каждую единицу груза.
Варианты заданий решения транспортной задачи в сетевой форме приведены в приложении.
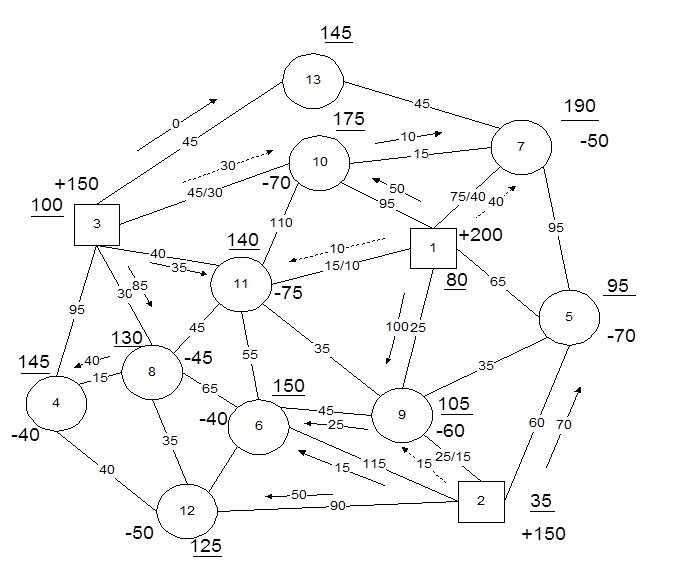 Рис. 10
Рис. 10
С каждой задачей ЛП можно связывать некоторую другую задачу (линейного программирования), такая задача будет называться двойственной или сопряженной по отношению к исходной или так называемой прямой.
В общем виде это означает, что некоторую математическую модель можно поставить различными системами (противоположными) и при этом получить правильный ответ.
Приведем определение двойственной задачи по отношению к прямой задаче ЛП, состоящей в определении max целевой функции вида
F = 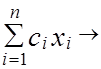 max
max
при ограничениях
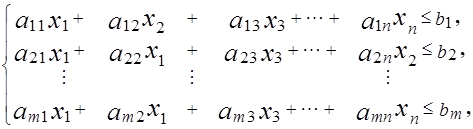 (1.63)
(1.63)
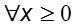 .
.
Задачу, состоящую в нахождении min целевой функции вида
F* = 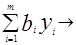 min
min
при условиях
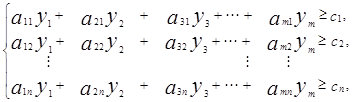 (1.64)
(1.64)
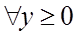 ,
,
называют двойственной по отношению к исходной задаче (1.63).
Задачи (1.63) и (1.64) образуют так называемую двойственную пару.
Сравнивая обе задачи, нетрудно заметить что:
1. Матрица из коэффициентов при переменных в исходной задаче
A = 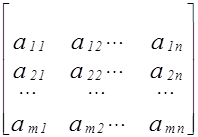
и аналогичная матрица в двойственной задаче
A¢ = 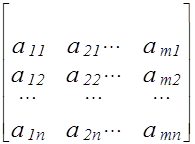
получаются друг из друга простой заменой строк столбцами с сохранением их порядка. Такую операцию называют транспонированием.
2. В исходной задаче n переменных и m ограничений, в двойственной, наоборот, m переменных и n ограничений.
3. В правых частях систем ограничений каждой из задач стоят коэффициенты целевой функции, взятой из другой задачи.
4. В систему ограничений исходной задачи входят неравенства типа 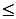 , причем в задаче требуется максимизировать целевую функцию F. В систему ограничений двойственной задачи входят неравенства типа
, причем в задаче требуется максимизировать целевую функцию F. В систему ограничений двойственной задачи входят неравенства типа 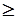 , причем в двойственной задаче требуется минимизировать целевую функцию F*.
, причем в двойственной задаче требуется минимизировать целевую функцию F*.
Двойственные пары задач делят на симметричные и несимметричные. В симметричной паре двойственных задач ограничения прямой задачи и соотношения двойственной задачи являются неравенствами вида 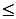 . Таким образом, переменные общих задач могут принимать только лишь неотрицательные значения.
. Таким образом, переменные общих задач могут принимать только лишь неотрицательные значения.
Заметим, что за исходную задачу можно взять любую задачу из этой пары, поскольку для дальнейшего решения это несущественно.
Приведенная ниже табл. 1.37. существенно облегчает процесс составления математической модели двойственной задачи.
В первой строке таблицы записываются все переменные исходной задачи, в первом столбце - все переменные двойственной задачи. В последней строке стоят коэффициенты целевой функции двойственной задачи. В клетках таблицы записаны коэффициенты при переменных исходной задачи.
 2014-02-09
2014-02-09 716
716








