Пусть 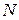 – общее число проданных договоров.
– общее число проданных договоров. 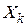 – выплаты по
– выплаты по 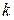 -му договору,
-му договору, 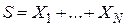 – суммарные выплаты по всему портфелю,
– суммарные выплаты по всему портфелю,  – относительная защитная надбавка, так что премия по одному договору равна
– относительная защитная надбавка, так что премия по одному договору равна 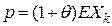 .
.
По условию,  . С другой стороны,
. С другой стороны,
 .
.
Поэтому
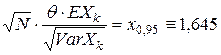 ,
,
где  – квантиль порядка 0,95 стандартного нормального (гауссовского) распределения.
– квантиль порядка 0,95 стандартного нормального (гауссовского) распределения.
Отсюда для искомого числа договоров имеем:
 .
.
Поскольку для индивидуального договора,
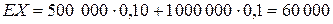 ,
,
 ,
,
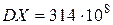 , искомое число договоров равно 590.
, искомое число договоров равно 590.
Задача 4.4. Компания ABC предполагает организовать групповое страхование жизни для своих сотрудников. Структура персонала приведена в следующее таблице:
| Профессиональный класс | Число сотрудников | Страховая сумма | Вероятность смерти |
| 0,1 | |||
| 0,2 | |||
| 0,1 | |||
| 0,2 |
Компания ABC предполагает внести в страховой фонд сумму, равную ожидаемым выплатам страховых возмещений.
Каждый сотрудник, в свою очередь, должен будет внести сумму, равную определенной доле 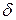 от размера ожидаемой выплаты. Размер этой доли определяется таким образом, чтобы с вероятностью 95% средств страхового фонда хватило для выплаты страховых возмещений.
от размера ожидаемой выплаты. Размер этой доли определяется таким образом, чтобы с вероятностью 95% средств страхового фонда хватило для выплаты страховых возмещений.
Определите размер взноса для работников четвертого профессионального класса.
Решение.
Пусть 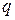 – вероятность смерти сотрудника,
– вероятность смерти сотрудника, 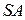 – размер страховой суммы. Поскольку индивидуальные потери по договору принимают только два значения: 0 с вероятностью
– размер страховой суммы. Поскольку индивидуальные потери по договору принимают только два значения: 0 с вероятностью 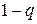 и
и 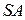 с вероятностью
с вероятностью 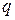 , среднее значение индивидуальных потерь есть
, среднее значение индивидуальных потерь есть 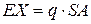 , а дисперсия –
, а дисперсия – 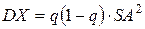 .
.
Предполагая независимость времен жизни сотрудников компании, можно подсчитать среднее и дисперсию суммарных выплат для каждого профессионального класса. Для этого нужно среднее (соответственно дисперсию) индивидуальных потерь умножить на число работников в классе:
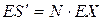
 .
.
Результаты расчетов поместим в таблицу:
| Класс | Число Сотрудников | 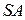
| 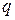
| 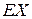
| 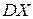
| 
| 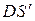
|
| 0,1 0,2 0,1 0,2 | 0,1 0,2 0,2 0,4 | 0,09 0,16 0,36 0,64 |
Чтобы получить среднее значение (дисперсию) суммарных выплат  для всего портфеля, нужно сложить средние (дисперсии) суммарных потерь для всех четырех профессиональных классов, так что
для всего портфеля, нужно сложить средние (дисперсии) суммарных потерь для всех четырех профессиональных классов, так что
 ,
, 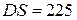 .
.
Размер страхового фонда равен . По условию, должно быть верно равенство
. По условию, должно быть верно равенство
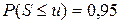 ,
,
или, что то же самое,
 .
.
Применяя гауссовское приближение для центрированной и нормированной величины общих выплат, мы имеем:
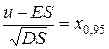 .
.
В рассматриваемой ситуации это равенство примет вид:
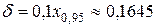 .
.
Соответственно защитная надбавка для работников четвертого профессионального класса равна 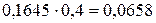 . Иначе говоря,
. Иначе говоря, 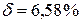 .
.
 2014-02-02
2014-02-02 673
673








