Например, вершины треугольника является его крайними точками, а все точки окружности – крайние точки круга.
8.5. Любую точку выпуклого множества можно представить в виде выпуклой комбинации его крайних точек.
8.6. Выпуклое множество будем называть многогранником или многогранным множеством, если оно содержит конечное количество крайних точек.
8.7. Система линейных ограничений, заданных уравнениями и (или) неравенствами, является выпуклым множеством.
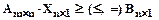 - выпуклое множество.
- выпуклое множество.
Пусть на оси ОХ даны две точки: 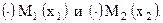 Тогда любая
Тогда любая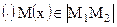 , делит отрезок
, делит отрезок 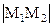 в отношении
в отношении 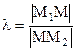 , при этом
, при этом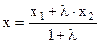 или
или 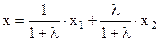 .
.
Если коэффициенты при  и
и 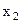 обозначить
обозначить 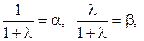 то получим: любая точка
то получим: любая точка 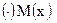 отрезка
отрезка 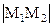 имеет координату х, удовлетворяющую условиям
имеет координату х, удовлетворяющую условиям 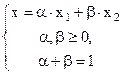 . Отсюда следует, что координата любой точки отрезка является линейной комбинацией координат его концов, при этом коэффициенты этой линейной комбинации неотрицательны и в сумме равны единице.
. Отсюда следует, что координата любой точки отрезка является линейной комбинацией координат его концов, при этом коэффициенты этой линейной комбинации неотрицательны и в сумме равны единице.
Определение Точку 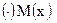 будем называть выпуклой комбинацией точек
будем называть выпуклой комбинацией точек 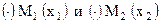 , если координата
, если координата 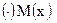 есть линейная комбинация координат точек
есть линейная комбинация координат точек 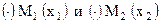 , причем коэффициенты этой линейной комбинации неотрицательны и в сумме равны единице.
, причем коэффициенты этой линейной комбинации неотрицательны и в сумме равны единице.
Следствие Отрезок между двумя точками можно рассматривать как множество всех точек, каждая из которых является выпуклой комбинацией его концов.
Пусть теперь даны две точки в n - мерном пространстве 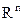 :
:  и
и 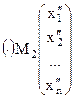 .
.
Определение Точку 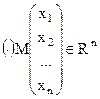 будем называть выпуклой комбинацией точек
будем называть выпуклой комбинацией точек 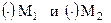 , если
, если
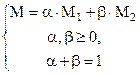 .
.
Определение Отрезком меду двумя точками 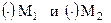 в
в 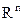 будем называть множество всех точек, являющихся их выпуклыми комбинациями.
будем называть множество всех точек, являющихся их выпуклыми комбинациями.
Пусть точки 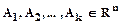 и числа
и числа  , тогда линейную комбинацию этих точек можно записать
, тогда линейную комбинацию этих точек можно записать
в виде точки 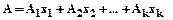 .
.
8.1. Линейную комбинацию точек будем называть выпуклой, если ее коэффициенты неотрицательны и их сумма = 1.
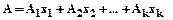 - выпукла
- выпукла 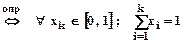 .
.
 2014-02-02
2014-02-02 1735
1735








