Пусть дано векторное пространство Rn.
Если существует правило (L), по которому любому вектору X Î Rn ставится в соответствие единственный вектор YÎ Rn, то такое правило называют оператором
или преобразованием в пространстве Rn, причем вновь полученный вектор Y называют образом данного вектора Х, а данный вектор Х называют прообразом в новь полученного вектора Y.
Зададим квадратную матрицу n-го порядка А. И пусть преобразование состоит в том, что каждому вектору X Î Rn ставится в соответствие вектор
7.1. 
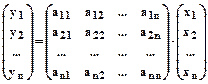 .
.
Матрицу А, осуществляющую это преобразование называют матрицей оператора L.
Если оператор задан квадратной матрицей А, то он обладает двумя очень важными свойствами:
7.2. При сложении прообразов образы тоже складываются
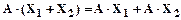 .
.
7.3. Если прообраз умножить на скаляр, то образ тоже умножится на этот скаляр
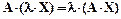 .
.
Если оператор обладает свойствами 7.2. и 73., то его называют линейным оператором. Следовательно, квадратную матрицу n -го порядка А, столбцами которой являются базисные векторы пространства Rn, можно рассматривать как матрицу линейного оператора. При этом переход к новому базису преобразует эту матрицу в матрицу 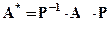 , где Р - матрица перехода к новому базису, причем координаты новых базисных векторов в старом базисе образуют ее столбцы.
, где Р - матрица перехода к новому базису, причем координаты новых базисных векторов в старом базисе образуют ее столбцы.
Векторному пространстве Rn могут принадлежать такие векторы Х, для которых действие линейного оператора с матрицей А равносильно умножению на число.
7.4. Если для данного вектора Х и данного линейного оператора с матрицей А найдется такое число l, для которого выполняется условие 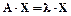 , то такой вектор Х называют собственным вектором матрицы А, а число l - ее собственным числом.
, то такой вектор Х называют собственным вектором матрицы А, а число l - ее собственным числом.
Если дана матрица линейного оператора А, то все собственные числа этой матрицы можно найти из матричного уравнения 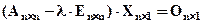 . В этом уравнении Е - единичная матрица, О - нулевой вектор. Оно равносильно однородной системе линейных уравнений, которая имеет ненулевое решение только в том случае, когда определитель системы равен нулю:
. В этом уравнении Е - единичная матрица, О - нулевой вектор. Оно равносильно однородной системе линейных уравнений, которая имеет ненулевое решение только в том случае, когда определитель системы равен нулю: 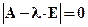 . Это уравнение называют характеристическим уравнением матрицы (оператора).
. Это уравнение называют характеристическим уравнением матрицы (оператора).
Левая часть характеристического уравнения преобразуется в многочлен n -ой степени относительно неизвестного l. Такое уравнение имеет ровно n корней среди которых могут быть или не быть вещественные корни. Если окажется, что все корни вещественные различные, то матрица имеет n различных вещественных собственных чисел.
Если матрица линейного оператора - симметрическая, то все ее собственные числа являются вещественными числами, а собственные векторы, соответствующие любым двум собственным числам ортогональны.
Если в качестве базиса можно выбрать собственные векторы, то переход к этому базису приведет матрицу линейного преобразования к диагональному виду:
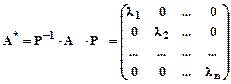 ,
,
где Р - матрица перехода к новому базису, столбцами которой являются собственные векторы, а li - их собственные числа.
Пример. Пусть линейный оператор задан матрицей 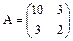 .
.
Тогда характеристическое уравнение этой матрицы имеет вид: 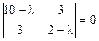 или
или 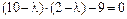 или
или 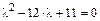 .
.
Корни этого уравнения 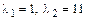 и являются собственными числами данной матрицы.
и являются собственными числами данной матрицы.
Теперь найдем собственные векторы для каждого собственного числа.
Пусть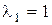 , а собственный вектор для него
, а собственный вектор для него 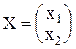 , тогда
, тогда 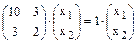 или
или 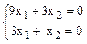
Определитель этой однородной системы отличен от нуля, следовательно она имеет бесчисленное множество решений, например: x1=-u; x2=3u, где u- параметр. Следовательно собственному числу 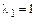 соответствует бесчисленное множество собственных векторов вида
соответствует бесчисленное множество собственных векторов вида 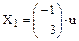 .
.
Аналогичные вычисления приводят к определению собственных векторов для 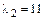 из системы
из системы 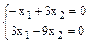
Получаем: x1=3v, x2=v, где v - параметр. Таким образом установили, что собственному числу 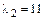 соответствует бесчисленное множество собственных векторов вида
соответствует бесчисленное множество собственных векторов вида 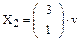 .
.
Уравнение 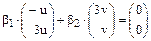 имеет единственное (нулевое) решение, следовательно векторы X1 и X2 линейно независимы.
имеет единственное (нулевое) решение, следовательно векторы X1 и X2 линейно независимы.
Скалярное произведение векторов 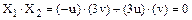 , следовательно векторы X1 и X2 ортогональны и значит они образуют ортогональный базис пространства R2.
, следовательно векторы X1 и X2 ортогональны и значит они образуют ортогональный базис пространства R2.
Пусть собственные векторы X1 и X2 образуют теперь новый базис, тогда матрица перехода к новому базису будет иметь вид: 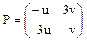 . Обратная ей матрица
. Обратная ей матрица 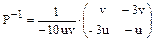 и в новом базисе матрица линейного оператора будет иметь вид:
и в новом базисе матрица линейного оператора будет иметь вид: 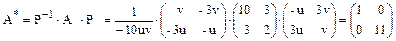 .
.
Таким образом матрица линейного оператора приведена к диагональному виду, причем диагональными элементами являются ее собственные числа.
 2014-02-02
2014-02-02 1992
1992
