В случае ламинарного движения вязкой жидкости в прямой трубе круглого сечения всю жидкость можно мысленно разбить на ряд кольцевых слоев, соосных с трубой (рисунок 8).
 | 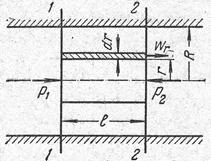 |
| а б Рисунок 8 - К определению распределения скоростей и расхода жидкости при ламинарном движении | |
Вследствие действия между слоями сил трения слои будут двигаться с неодинаковыми скоростями. Центральный цилиндрический слой у оси трубы имеет максимальную скорость, но, по мере удаления от оси, скорость элементарных кольцевых слоев будет уменьшаться. Непосредственно у стенки скорость жидкости равна нулю.
Выделим в потоке жидкости, ламинарно движущемся по трубе радиусом R цилиндрический слой длиной l и радиусом r (рисунок 8 б).
Движение слоя происходит под действием разности сил давления Р1 и Р2 с обеих торцевых сторон цилиндра:
 ,
,
где р1 и р2 – гидростатические давления в сечениях 1-1 и 2-2.
Движению цилиндра (жидкости) оказывает сопротивление сила внутреннего трения Т:
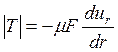 ,
,
Где ur – скорость движения жидкости вдоль оси цилиндра на расстоянии r от оси;
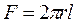 - наружная поверхность цилиндра;
- наружная поверхность цилиндра;
μ – вязкость жидкости.
Знак минус указывает на убывание скорости с увеличением радиуса r(при r=R величина ur= 0).
При установившемся движении разность сил давления Р1-Р2 затрачиваемая на преодоление силы трения Т, и сумма проекций всех этих сил на ось потока должна быть равна нулю. Вследствие трения движение рассматриваемого цилиндрического слоя тормозится, значит, сила трения, приложенная к его боковой поверхности, направлена противоположно разности Р1-Р2 и проектируется на ось, направление которой совпадает с направлением движения, со знаком минус. Следовательно:
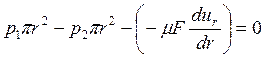 ,
,
Или
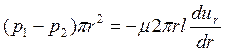 ,
,
Откуда после сокращения и разделения переменных, получим:
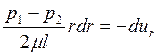 ,
,
Переходя ко всему объему жидкости в трубе, проинтегрируем это дифференциальное уравнение, учитывая, что радиус в левой части уравнения изменится от rдо r=R, а переменная скорость в правой части – от u=ur до u=0 (у стенки, где r=R).
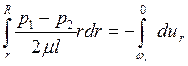 ,
,
Тогда:
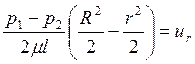 ,
,
или
 ,
,
Скорость имеет максимальное значение на оси трубы, где r=0.
 ,
,
Скорость движения жидкости:
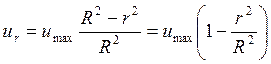 ,
,
Последнее уравнение представляет собой закон Стокса, выражающий параболитическое распределение скоростей в сечении трубопровода при ламинарном движении.
Для определения расхода жидкости при ламинарном движении рассмотрим элементарное кольцевое сечение (рисунок 8 б) с внутренним радиусом uи внешним радиусом (r+dr), площадь которого равна
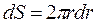
Объемный расход жидкости через это сечение составляет:
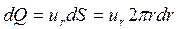 ,
,
Или
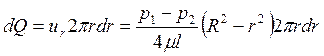 ,
,
Интегрируя последнее уравнение, получим расход жидкости через трубу:
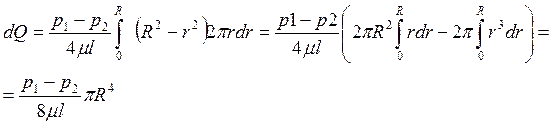 ,
,
Подставляя вместо R диаметр трубы d=2R и обозначая (р1-р2)=∆р, получаем:
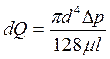 ,
,
Уравнения, определяющие расход жидкости при ее ламинарном движении по круглой прямой трубе носит название уравнения Пуазейля.
При ламинарном потоке в трубе средняя скорость жидкости равна половине скорости по оси трубы:
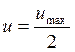 ,
,
 2014-02-02
2014-02-02 3567
3567
