2014-02-02
3915
Одной из основных задач дифференциального исчисления является отыскание производной заданной функции. Здесь мы будем решать обратную задачу, а именно: известна производная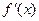 
от функции 
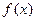. Требуется найти саму функцию 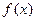. С точки зрения механической это означает, что по известной скорости движения материальной точки необходимо восстановить закон е. движения.
Определение 1. Функция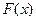 
называется первообразной для функции 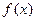на интервале 
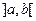. Если для любого х из этого интервала выполняется равенство
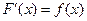. (1)
Пример 1.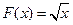 
есть первообразная для функции 
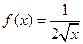на интервале 
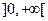, так как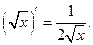 
Пример 2.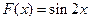 
является первообразной для функции 
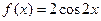на интервале 
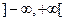, поскольку 
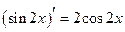для любого х из этого интервала.
Задача отыскания по данной функции f(x) её первообразной решается однозначно. Имеет место следующая
Теорема 1. Если 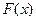– первообразная для функции 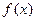на интервале 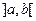, то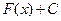 
, где С – произвольная постоянная, также будет первообразной для .
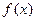Теорема 2. Есл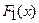и 
и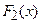 
– две первообразные для функции 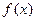на интервале 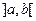, то– 
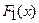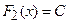на 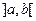, где С – некоторая постоянная.
Доказательство: По условию 
. Составим функцию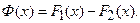 
Очевидно, что 
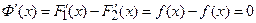для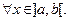 
Отсюда, по следствию из теоремы Лагранжа, заключаем, что 
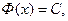т. е.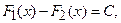 
что и требовалось доказать.
Определение 2. Если функция 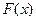– первообразная для функции 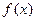на интервале 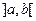, то множество функций 
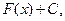где С – произвольная постоянная, называется неопределенным интегралом от функции 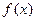и обозначается символом
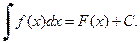(2)
При этом знак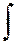 
называется знаком неопределенного интеграла; функция 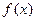– подынтегральной функцией; 
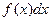– подынтегральным выражением, а переменная х – переменной интегрирования. Символ 
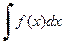обозначает, таким образом, совокупность всех первообразных для функции 
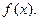но иногда мы будем понимать его как любой элемент из этой совокупности, т. е. как какую-то из первообразных.
Операцию нахождения неопределенного интеграла будем называть интегрированием функции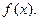
Интегрирование представляет собой операцию, обратную дифференцированию. Для того, чтобы проверить, правильно ли выполнено интегрирование, достаточно продифференцировать результат и получить при этом подынтегральную функцию.
Отметим без доказательства, что имеет место
Теорема 3. Если 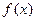непрерывна на 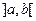, то для неё существует первообразная на 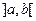, а следовательно, и неопределенный интеграл.
