Доказательство.
Свойства неопределенного интеграла
10. Производная от неопределенного интеграла равна подынтегральной функции:
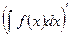 =
=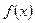 . (1.4)
. (1.4)
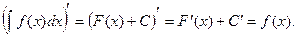
20. Дифференциал от неопределённого интеграла равен подынтегральному выражению:
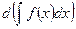
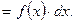 (1.5)
(1.5)
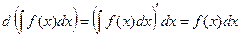 .
.
30. Неопределенный интеграл от дифференциала некоторой функции равен сумме этой функции и произвольной постоянной:
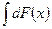 =
=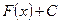 . (1.6)
. (1.6)
Свойство очевидно.
40. Аддитивность неопределенного интеграла. Неопределенный интеграл от суммы (разности) функций равен сумме (разности) неопределенных интегралов от этих функций:
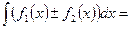
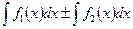 .
.
Доказательство. Для доказательства свойства найдем производную от правой части равенства:
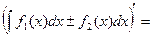
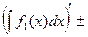
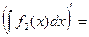
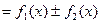 .
.
Мы получили подынтегральную функцию интеграла 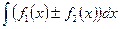 , что и доказывает данное свойство.
, что и доказывает данное свойство.
50. Однородность неопределённого интеграла. Постоянный множитель, отличный от нуля, можно выносить за знак неопределённого интеграла:
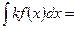
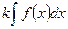 ,
, 
 2014-02-02
2014-02-02 3107
3107
