Геометрические вероятности. Теорема сложения вероятностей. Противоположные события. Условные вероятности. Теорема умножения вероятностей. Независимые события. Вероятность появления хотя бы одного события.
Лекция 2.
Одним из недостатков классического определения вероятности является то, что оно неприменимо к испытаниям с бесконечным количеством исходов. В таких случаях можно воспользоваться понятием геометрической вероятности.
Пусть на отрезок L наудачу брошена точка. Это означает, что точка обязательно попадет на отрезок L и с равной возможностью может совпасть с любой точкой этого отрезка. При этом вероятность попадания точки на любую часть отрезка L не зависит от расположения этой части на отрезке и пропорциональна его длине. Тогда вероятность того, что брошен-ная точка попадет на отрезок l, являющийся частью отрезка L, вычисляется по формуле:
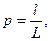 (2.1)
(2.1)
где l – длина отрезка l, а L – длина отрезка L.
Можно дать аналогичную постановку задачи для точки, брошенной на плоскую область S и вероятности того, что она попадет на часть этой области s:
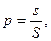 (2.1`)
(2.1`)
где s – площадь части области, а S – площадь всей области.
В трехмерном случае вероятность того, что точка, случайным образом расположенная в теле V, попадет в его часть v, задается формулой:
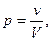 (2.1``)
(2.1``)
где v – объем части тела, а V – объем всего тела.
Пример 1. Найти вероятность того, что точка, наудачу брошенная в круг, не попадет в правильный шестиугольник, вписанный в него.
Решение. Пусть радиус круга равен R, тогда сторона шестиугольника тоже равна R. При этом площадь круга 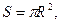 а площадь шестиугольника
а площадь шестиугольника 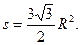 Следовательно,
Следовательно,
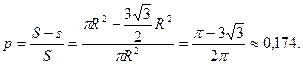
Пример 2. На отрезок АВ случайным образом брошены три точки: С, D и М. Найти вероятность того, что из отрезков АС, АD и АМ можно построить треугольник.
Решение. Обозначим длины отрезков АС, АD и АМ через x, y и z и рассмотрим в качестве возможных исходов множество точек трехмерного пространства с координатами (х, у, z). Если принять длину отрезка равной 1, то эти множество возможных исходов представляет собой куб с ребром, равным 1. Тогда множество благоприятных исходов состоит из точек, для координат которых выполнены неравенства треугольника: x + y > z, x + z > y, y + z > x. Это часть куба, отрезанная от него плоскостями x + y = z, x + z = y, y + z = x
х 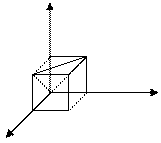 Рис.1.
Рис.1.
(одна из них, плоскость x + y = z, проведена на рис.1). Каждая такая плоскость отделяет от куба пирамиду, объем которой равен 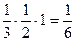 . Следовательно, объем оставшейся части
. Следовательно, объем оставшейся части
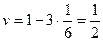 . Тогда
. Тогда 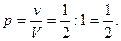
Теорема 2.1 (теорема сложения). Вероятность р (А + В) суммы событий А и В равна
Р (А + В) = р (А) + р (В) – р (АВ). (2.2)
Доказательство.
Докажем теорему сложения для схемы случаев. Пусть п – число возможных исходов опыта, тА – число исходов, благоприятных событию А, тВ – число исходов, благопри-ятных событию В, а тАВ – число исходов опыта, при которых происходят оба события (то есть исходов, благоприятных произведению АВ). Тогда число исходов, при которых имеет место событие А + В, равно тА + тВ – тАВ (так как в сумме (тА + тВ) тАВ учтено дважды: как исходы, благоприятные А, и исходы, благоприятные В). Следовательно, вероятность суммы можно определить по формуле (1.1):
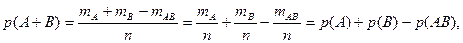
что и требовалось доказать.
Следствие 1. Теорему 2.1 можно распространить на случай суммы любого числа событий. Например, для суммы трех событий А, В и С
Р (А + В + С) = р (А) + р (В) + р (С) – р (АВ) – р (АС) – р (ВС) + р (АВС) (2.3)
и т.д.
Следствие 2. Если события А и В несовместны, то тАВ = 0, и, следовательно, вероятность суммы несовместных событий равна сумме их вероятностей:
Р (А + В) = р (А) + р (В). (2.4)
Определение 2.1. Противоположными событиями называют два несовместных события, образующих полную группу. Если одно из них назвать А, то второе принято обозначать 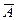 .
.
Замечание. Таким образом, 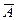 заключается в том, что событие А не произошло.
заключается в том, что событие А не произошло.
Теорема 2.2. Сумма вероятностей противоположных событий равна 1:
р (А) + р (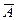 ) = 1. (2.5)
) = 1. (2.5)
Доказательство.
Так как А и 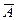 образуют полную группу, то одно из них обязательно произойдет в результате опыта, то есть событие А +
образуют полную группу, то одно из них обязательно произойдет в результате опыта, то есть событие А +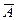 является достоверным. Следовательно,
является достоверным. Следовательно,
Р (А +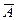 ) = 1. Но, так как А и
) = 1. Но, так как А и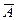 несовместны, из (2.4) следует, что Р (А +
несовместны, из (2.4) следует, что Р (А +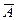 ) = р (А) + р (
) = р (А) + р (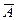 ). Значит, р (А) + р (
). Значит, р (А) + р (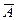 ) = 1, что и требовалось доказать.
) = 1, что и требовалось доказать.
Замечание. В ряде задач проще искать не вероятность заданного события, а вероятность события, противоположного ему, а затем найти требуемую вероятность по формуле (2.5).
Пример. Из урны, содержащей 2 белых и 6 черных шаров, случайным образом извлека-ются 5 шаров. Найти вероятность того, что вынуты шары разных цветов.
Решение. Событие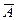 , противоположное заданному, заключается в том, что из урны вынуто 5 шаров одного цвета, а так как белых шаров в ней всего два, то этот цвет может быть только черным. Множество возможных исходов опыта найдем по формуле (1.5):
, противоположное заданному, заключается в том, что из урны вынуто 5 шаров одного цвета, а так как белых шаров в ней всего два, то этот цвет может быть только черным. Множество возможных исходов опыта найдем по формуле (1.5):
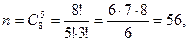
а множество исходов, благоприятных событию 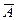 - это число возможных наборов по 5 шаров только из шести черных:
- это число возможных наборов по 5 шаров только из шести черных:
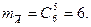
Тогда 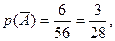 а
а 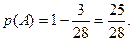
 2014-02-02
2014-02-02 999
999








