Рис. 4.16
Рис. 4.14
Рис. 4.7
Рис. 4.3
Таблица 2.2
| ПРАВИЛО | ИСХОДНАЯ ЦЕПЬ | ЭКВИВАЛЕНТНАЯ ЦЕПЬ |
| 1.Перестановка точек cумми-рования (от перестановки слагаемых сумма не меняется) | 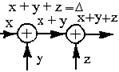 | 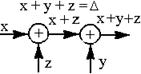 |
| 2.Изменение знаков входных и выходных переменных сумматора (изменение знаков обоих частей уравнения на противоположные) | 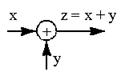 | 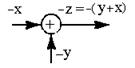 |
| 3.Порядок соединения cум-маторов можно изменять (от перестановки мест и взаимной группировки слагаемых сумма не меняется) | 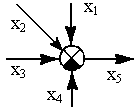 | 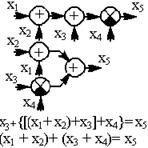 |
| 4.Любой сигнал можно последова-тельно прибавить, а затем вычесть | 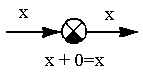 | 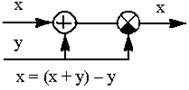 |
| 5.Порядок операций можно менять (от перестановки мест сомножи-телей произведение не меняется) | 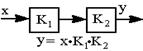 | 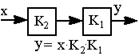 |
| 6.Последовательное выполнение прямой и обратной операций не вносит изменений в схему (результат не изменится, если переменную умножить и поделить на одно и то же число) | 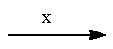 | 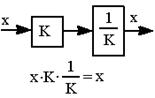 |
| 7.Порядок выполнения операций и суммирования можно изменять | 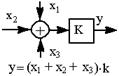 | 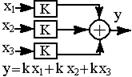 |
| 8.Порядок выполнения операций и точки разветвления можно менять | 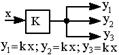 | 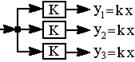 |
| 9.Перемещение динамического звена вперёд через сумматор или перемещение сумматора назад через динамическое звено (вынесение сомножителя за скобку) | 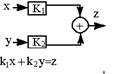 | 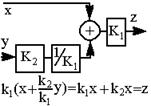 |
| 10.Перемещение динамического звена назад через точку разветвления или перемещение точки разветвления вперед через динамическое звено (умножение и деление уравнений на одно и то же число) | 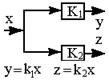 | 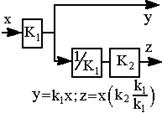 |
| 11.Перестановка точек съема (прибавление или вычитание нуля) | 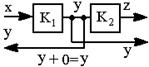 | 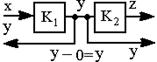 |
| 12.Перенос точки суммирования с входа звена на его выход (умножение скобки на постоянный коэффициент) | 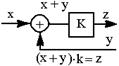 | 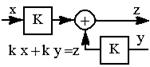 |
| 13.Перенос точки суммирования с выхода звена на его вход (вынесение сомножителя за скобку) | 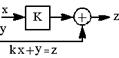 | 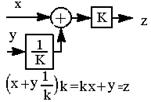 |
| 14.Перенос точки съема с входа звена на его выход (см. правила 6 и 10) | 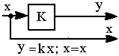 | 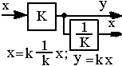 |
| 15.Перенос точки съема с выхода звена на его вход (см. правило 14) | 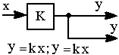 | 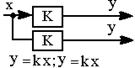 |
| 16.Применение усилителя с бесконечным усилением для инверсии операции. Число полюсов функции равно числу нулей этой функции | 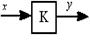 К=у/х К=у/х | 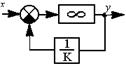 К = у/х К = у/х |
| 17.Исключение неединичной обратной связи (преобразование структурной схемы проведено на основании правил 13 и 5) | 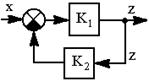 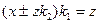 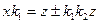 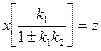 | 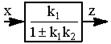 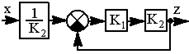 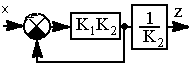 |
| 18.Преобразование параллельной связи к единичной обратной связи | 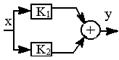 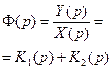  | 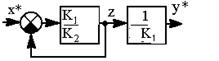 обратная эквивалентная схема обратная эквивалентная схема 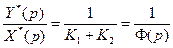 |
Пример. На рис. 2.3 а представлена структурная схема, которую необходимо преобразовать к простейшему виду рис.2.3 б. Прежде чем объединять отдельные звенья, в данном случае необходимо освободиться от перекрестных связей, для этого можно перенести точку (а) в точку (б) (правило 14) и объединить между собой звенья, соединённые последовательно, параллельно и с помощью обратной связи, пользуясь формулами.
|
|
|
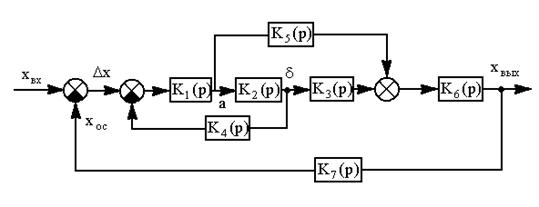
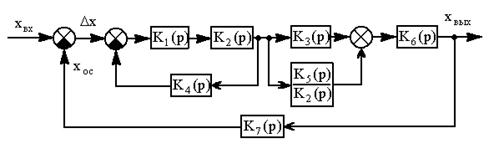
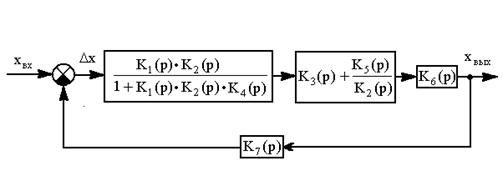
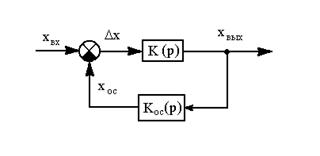
Рис.2.3
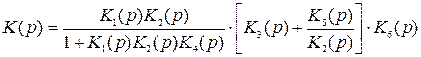 ;
;
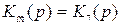 .
.
2.9. ПЕРЕДАТОЧНЫЕ ФУНКЦИИ ЗАМКНУТОЙ И РАЗОМКНУТОЙ
СИСТЕМЫ
Для любой САУ можно составить несколько передаточных функций. Их количество определяется количеством входных воздействий и интересующих выходных переменных. В ТАУ пользуются тремя основными видами передаточных функций.
|
|
|
Основная передаточная функция
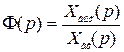 (2.61)
(2.61)
определяется как отношение изображений выходной величины и входного воздействия при нулевых начальных условиях.
Передаточная функция по ошибке
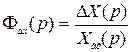 (2.62)
(2.62)
определяется как отношение изображений сигнала ошибки и входного воздействия при нулевых начальных условиях.
Передаточная функция по обратной связи
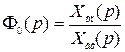 (2.63)
(2.63)
определяется как отношение изображений сигнала главной обратной связи и входного сигнала при нулевых начальных условиях.
Кроме перечисленных передаточных функций замкнутой САУ в ТАУ пользуются передаточной функцией разомкнутой системы
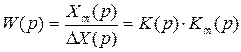 , (2.64)
, (2.64)
которая определяется как отношение изображений сигналов главной обратной связи и ошибки при нулевых начальных условиях и возмущающих воздействиях, равных нулю. Передаточная функция разомкнутой системы имеет большое значение в ТАУ, гак как многие методы анализа и синтеза основаны на использовании именно этой функции.
Установим связь между передаточными функциями замкнутой и разомкнутой системы. На основании (2.61), (2.62), (2.63) запишем
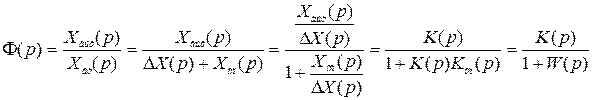 ; (2.66)
; (2.66)
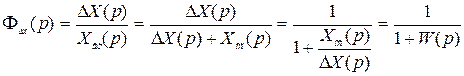 ; (2.67)
; (2.67)
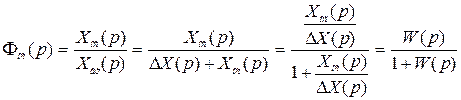 . (2.68)
. (2.68)
Формулы (2.66)–(2.68) позволяют по известной передаточной функции разомкнутой системы определить любую передаточную функций замкнутой системы.
3. УСТАНОВИВШИЕСЯ РЕЖИМЫ
СИСТЕМ АВТОМАТИЧЕСКОГО УПРАВЛЕНИЯ
ЛЕКЦИЯ 6
План лекции:
1. Понятие об установившемся режиме.
2. Точность САУ в установившемся режиме.
3. Установившиеся ошибки следящих систем.
4. Коэффициенты ошибок.
5. Рекомендуемая литература [1, 3, 7].
3.1. ТОЧНОСТЬ САУ В УСТАНОВИВШЕМСЯ РЕЖИМЕ
Установившимся называют режим работы системы управления после затухания собственных колебаний. При этом переменные величины САУ или остаются неизменными, или находятся в вынужденном движении, характер которого определяется видом внешнего воздействия. Математически в линейных системах этому соответствует обращение в нуль экспоненциальных составляющих решений дифференциальных уравнений, описывающих поведение системы, что имеет место при 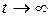 .
.
Практически можно считать режим установившимся, когда экспоненциальные составляющие, характеризующие свободное движение системы, станут настолько малыми, что полное решение уравнений лишь незначительно (обычно на 5% от максимального значения соответствующей функции) будет отличаться от его частного решения, определяющего вынужденное движение системы. Точность САУ в установившемся режиме характеризуется ошибками системы при различных воздействиях - постоянном возмущающем (в частном случае, единичном), а также управляющих и возмущающих, изменяющихся по определённым законам.
Необходимые расчётные соотношения для вычисления установившихся ошибок САУ могут быть определены при помощи теоремы операционного исчисления о предельном значении функции. Эта теорема утверждает, что если 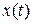 есть оригинал операторного изображения
есть оригинал операторного изображения 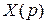 , т. е.
, т. е. 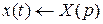 и если
и если 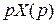 есть аналитическая функция комплексного переменного
есть аналитическая функция комплексного переменного 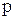 на мнимой оси и в правой полуплоскости, то
на мнимой оси и в правой полуплоскости, то
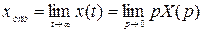 , (3.1)
, (3.1)
где 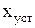 - установившееся значение функции
- установившееся значение функции 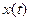 .
.
Передаточную функцию замкнутой САУ в общем виде можно представить следующим образом:
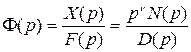 , (3.2)
, (3.2)
где 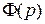 может быть любая из рассмотренных в предыдущей главе передаточных функций замкнутой САУ;
может быть любая из рассмотренных в предыдущей главе передаточных функций замкнутой САУ;
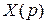 - изображение любой интересующей нас переменной, чаще всего регулируемой величины
- изображение любой интересующей нас переменной, чаще всего регулируемой величины 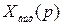 , сигнала ошибки
, сигнала ошибки 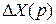 или сигнала главной обратной связи
или сигнала главной обратной связи 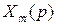 ;
;
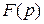 - любое внешнее воздействие (управляющее или возмущающее) приложенное к любой точке системы;
- любое внешнее воздействие (управляющее или возмущающее) приложенное к любой точке системы;
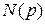 - полином числителя передаточной функции
- полином числителя передаточной функции 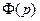 , не содержащий нулевых корней;
, не содержащий нулевых корней;
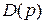 - полином знаменателя передаточной функции
- полином знаменателя передаточной функции 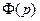 (характеристический полином);
(характеристический полином);
|
|
|
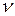 - порядок астатизма системы.
- порядок астатизма системы.
Для статической системы 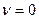 и передаточная функция (3.2) принимает вид
и передаточная функция (3.2) принимает вид
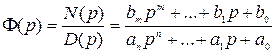 , (3.3)
, (3.3)
где 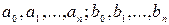 - постоянные коэффициенты;
- постоянные коэффициенты;
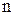 - порядок характеристического уравнения
- порядок характеристического уравнения 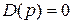 , причём
, причём 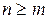 . Пусть на САУ действует некоторое постоянное (или медленно изменяющееся по сравнению со временем протекания переходных процессов) воздействие
. Пусть на САУ действует некоторое постоянное (или медленно изменяющееся по сравнению со временем протекания переходных процессов) воздействие 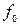 (в частном случае
(в частном случае 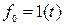 единичное скачкообразное воздействие);
единичное скачкообразное воздействие);
А. Для статических систем в соответствии с выражениями (3.1) и (3.3) можно написать
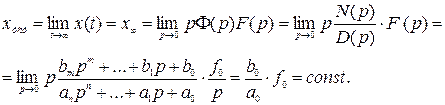 (3.4)
(3.4)
Формулу (3.4) можно использовать для вычисления установившихся ошибок статических САУ вызванных постоянным воздействием 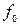 .
.
Б. Для астатических систем в соответствии с выражениями (3.1) и (3.2) можно записать
 (3.5)
(3.5)
Следовательно, в астатических системах установившаяся ошибка, вызванная постоянным воздействием, равняется нулю. Полученный вывод справедлив лишь для идеализированных систем, в которых не учитываются такие факторы, как зона нечувствительности, сухое трение, люфт и другие нелинейности.
Следует иметь в виду, что одна и та же система может быть астатической по отношению к одному воздействию и статической по отношению к другому воздействию.
В реальных системах учёт влияния этих факторов производится из условия компенсации соответствующего постоянного возмущения за счет увеличения статической (установившейся) ошибки системы.
Так, статическая ошибка следящей системы при заданном статическом моменте 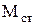 на валу исполнительного двигателя определяется из условия
на валу исполнительного двигателя определяется из условия
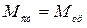 ,
,
где 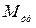 - момент трогания двигателя, развиваемый последним в заторможенном состоянии при определённой величине ошибки
- момент трогания двигателя, развиваемый последним в заторможенном состоянии при определённой величине ошибки 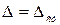 . Считая
. Считая 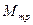 пропорциональным напряжению, подаваемому на двигатель, можно записать
пропорциональным напряжению, подаваемому на двигатель, можно записать
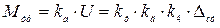 , (3.6)
, (3.6)
где 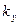 - коэффициент усиления усилителя по напряжению;
- коэффициент усиления усилителя по напряжению;
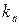 - передаточный коэффициент двигателя по моменту;
- передаточный коэффициент двигателя по моменту;
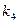 - передаточный коэффициент чувствительного элемента.
- передаточный коэффициент чувствительного элемента.
Приравнивая 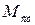 и
и 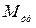 , получим
, получим
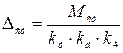 . (3.7)
. (3.7)
3.2. УСТАНОВИВШИЕСЯ ОШИБКИ СЛЕДЯЩИХ СИСТЕМ
Следящие системы обычно являются астатическими системами с астатизмом первого порядка, работающими при переменном управляющем воздействии. Для таких систем в установившемся режиме наиболее характерным является изменение входной величины по линейному закону с постоянной скоростью 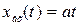 , чему соответствует операторное изображение вида
, чему соответствует операторное изображение вида
|
|
|
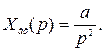 (3.8)
(3.8)
На основании выражений (3.1), (3.2), (3.8) при 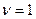 будем иметь
будем иметь
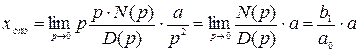 . (3.9)
. (3.9)
Установившуюся ошибку следящей системы при входном сигнале, изменяющимся с постоянной скоростью, называют скоростной ошибкой. Обозначив скоростную ошибку 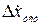 , а отношение
, а отношение  через
через 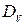 , на основании (3.9), окончательно получим
, на основании (3.9), окончательно получим
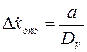 . (3.10)
. (3.10)
Постоянная величина
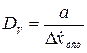 (3.11)
(3.11)
называется добротностью следящей системы по скорости и имеет размерность с-1. Она показывает величину установившейся скорости выходной оси следящей системы, развиваемой на единицу скоростной ошибки.
В следящей системе с астатизмом второго порядка (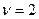 ) скоростная ошибка равняется нулю, вследствие этого установившуюся ошибку определяют при изменении входной величины по квадратичному закону с постоянным ускорением
) скоростная ошибка равняется нулю, вследствие этого установившуюся ошибку определяют при изменении входной величины по квадратичному закону с постоянным ускорением 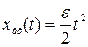 . При этом
. При этом
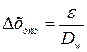 ;
; 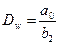 , (3.12)
, (3.12)
где 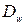 – добротность следящий системы по ускорению, имеющая размерность с- 2.
– добротность следящий системы по ускорению, имеющая размерность с- 2.
Величины 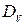 и
и 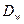 зависят от параметров САУ. В одноконтурных системах без местных обратных связей они определяются как произведения передаточных коэффициентов звеньев системы. В более сложных САУ при определении установившихся ошибок удобнее пользоваться не готовыми формулами, а теоремой о предельном значении функции (3.1). Применяя её к операторному изображению ошибки следящей системы в каждом конкретном случае.
зависят от параметров САУ. В одноконтурных системах без местных обратных связей они определяются как произведения передаточных коэффициентов звеньев системы. В более сложных САУ при определении установившихся ошибок удобнее пользоваться не готовыми формулами, а теоремой о предельном значении функции (3.1). Применяя её к операторному изображению ошибки следящей системы в каждом конкретном случае.
В общем случае, если 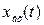 имеет произвольную форму и имеет конечное число производных, то ошибку системы можно определить следующим образом. Найдём изображение ошибки
имеет произвольную форму и имеет конечное число производных, то ошибку системы можно определить следующим образом. Найдём изображение ошибки
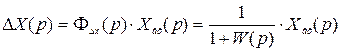 , (3.13)
, (3.13)
где 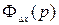 - передаточная функция замкнутой системы по ошибке;
- передаточная функция замкнутой системы по ошибке;
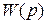 - передаточная функция разомкнутой системы;
- передаточная функция разомкнутой системы;
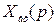 - изображение воздействия (задающего или возмущающего).
- изображение воздействия (задающего или возмущающего).
Разложим передаточную функцию по ошибке в ряд по возрастающим степеням комплексной величины 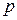
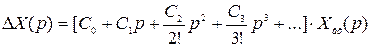 . (3.14)
. (3.14)
Этот ряд сходится при малых значениях 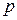 , т.е. при достаточно большом
, т.е. при достаточно большом 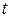 , что соответствует установившемуся процессу.
, что соответствует установившемуся процессу.
Переходя от изображения (3.1) к оригиналу, получаем формулу для установившейся ошибки
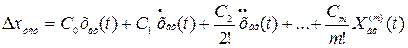 . (3.15)
. (3.15)
Величины 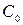 ,
, ,…,Сm называют коэффициентами ошибок. Они могут определяться согласно общему правилу разложения функции в ряд Тейлора по формулам:
,…,Сm называют коэффициентами ошибок. Они могут определяться согласно общему правилу разложения функции в ряд Тейлора по формулам:
 ;
; 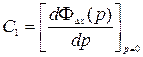 ; ………;
; ………; 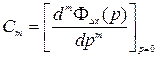 .
.
Так как передаточная функция по ошибке представляет собой дробно-рациональную функцию, то коэффициенты ошибок можно более просто получить делением числителя на знаменатель и сравнением получающегося ряда с выражением (3.14).
Коэффициент 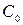 отличен от нуля только в статических системах.
отличен от нуля только в статических системах.
В системах с астатизмом первого порядка
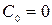 ;
; 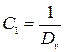 .
.
В системах с астатизмом второго порядка
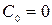 ;
; 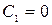 ;
;  .
.
Если задающее воздействие имеет ограниченное число производных, то ряд будет иметь ограниченное число членов.
Пример. Определить первые три коэффициента ошибки по задающему воздействию, если передаточная функция разомкнутой системы имеет вид
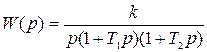 .
.
Найдем передаточную функцию по ошибке
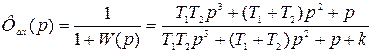
Делим числитель на знаменатель и получаем ряд
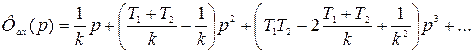
Таким образом, 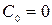 ;
; 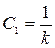 ;
; 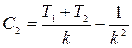 .
.
Если задающее воздействие в этой системе меняется по закону
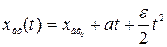 ;
; 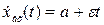 ;
; 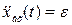 ,
,
то установившаяся ошибка будет равна
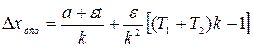 .
.
ЛЕКЦИЯ 7
План лекции:
1. Частотные характеристики САУ.
2. Логарифмические амплитудные и фазовые частотные характеристики.
3. Рекомендуемая литература [1, 8].
ЧАСТОТНЫЕ ХАРАКТЕРИСТИКИ САУ
Частотные характеристики характеризуют установившиеся вынужденные колебания на выходе системы или звена, вызванные гармоническим воздействием на входе.
Для аналитического определения частотных характеристик будем считать, что входное воздействие изменяется по следующему закону:
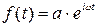 . (3.16)
. (3.16)
При заданном воздействии (3.16) решение линейного дифференциального уравнения
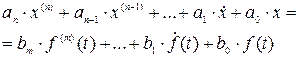 (3.17)
(3.17)
можно искать в следующем виде:
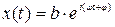 . (3.18)
. (3.18)
где 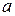 и
и 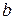 - амплитуды входного воздействия и выходной величины;
- амплитуды входного воздействия и выходной величины;
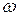 - круговая частота воздействия;
- круговая частота воздействия;
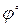 - сдвиг по фазе выходного сигнала относительно входного. На основании (3.16) и (3.18) можно записать
- сдвиг по фазе выходного сигнала относительно входного. На основании (3.16) и (3.18) можно записать

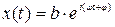
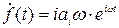
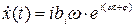
…………………………………… (3.19)
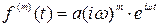

Подставив выражения (3.19) в уравнение (3.17), получим
 ,
,
или
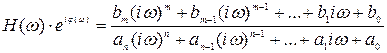 . (3.20)
. (3.20)
Выражение (3.20) представляет собой амплитудно-фазовую частотную характеристику (АФЧХ) САУ.
Сравнение её с передаточной функцией
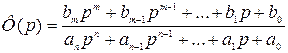
показывает, что аналитическое выражение АФЧХ получается путём формальной замены в соответствующей передаточной функции оператора 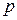 на
на 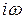 . Таким образом, имея передаточную функцию системы или звена, можно легко получить выражение для АФЧХ этой системы или звена:
. Таким образом, имея передаточную функцию системы или звена, можно легко получить выражение для АФЧХ этой системы или звена:
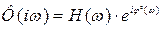 . (3.21)
. (3.21)
Выражение (3.21) иногда называют ещё комплексной или частотной передаточной функцией.
Для экспериментального определения АФЧХ входное воздействие целесообразно изменять по гармоническому закону
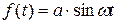 .
.
Тогда частное решение линейного уравнения (3.17) необходимо искать в виде
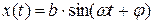 . (3.22)
. (3.22)
Нетрудно показать, что выражение для АФЧХ в этом случае получается точно такое же, как и в предыдущем.
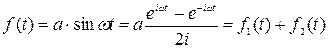 ,
,
где
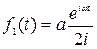 ;
; 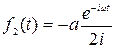 .
.
Тогда
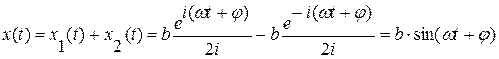
и выражение для АФЧХ 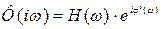 принимает вид (3.20).
принимает вид (3.20).
АФЧХ (3.20) представляет собой комплексную функцию, следовательно,
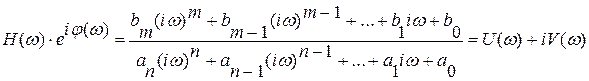 ,
,
где 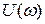 - действительная часть АФЧХ,
- действительная часть АФЧХ, 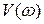 - мнимая часть АФЧХ.
- мнимая часть АФЧХ.
 2014-02-02
2014-02-02 2314
2314








