2014-02-02
1733
Лекция 30
Лекция 29
Лекция 28
Лекция 27
Лекция 26
Лекция 25
Лекция 24
Лекция 23
Лекция 22
Лекция 21
Лекция 20
Лекция 19
Лекция 18
Лекция 17
Лекция 16
5.7. Интегральные оценки качества ………………………..…………….….97
5.8. Косвенные оценки качества, связанные с видом частотных
характеристик………………………………………………………….…100
6. ДИНАМИЧЕСКИЙ СИНТЕЗ САУ……………………………..…....……..…102
6.1. Общие понятия синтеза САУ……………………………….………..…..102
6.2. Этапы синтеза САУ…………………………………………….................103
6.3. Требования, предъявляемые к динамическим свойствам САУ………..104
6.4. Методы коррекции динамических свойств САУ……………………….105
6.5. Динамический синтез САУ, основанный на построении желаемой
ЛАФЧХ……………………………………………………………………..108
6.6. Синтез последовательного корректирующего устройства……………..112
6.7. Синтез параллельного корректирующего устройства………………….113
7. МЕТОДЫ СИНТЕЗА, ОСНОВАННЫЕ НА ТЕОРИИ ПРОСТРАНСТВА
СОСТОЯНИЙ…..…………………………………………………………….115
7.1. Уравнения системы в пространстве состояний………………………....115
7.2. Коррекция системы в пространстве состояний………………………..121
7.3. Прямой корневой метод синтеза доминантного типа…………………122
7.4. Прямой корневой метод синтеза САУ по координатам
пространства состояний………………………………………..…..……123
7.5. Прямой метод синтеза корректирующей обратной связи следящей
системы………………………………………………………………..….125
8. Системы автоматического управления
при случайных воздействиях…………………….………….…….127
8.1. Детерминированные и случайные функции…………………………....127
8.2. Основные вероятностные характеристики случайных процессов….…128
8.3. Стацонарные случайные процессы. Эргодическая гипотеза…………..133
8.4. Спектральная плотность стационарного эргодического
случайного процесса……………………………………………………..137
8.5. Свойства корреляционных функций и спектральных плотностей
стационарных эргодических случайных процессов………………………...140
8.6. Статистические характеристики случайных типовы процессов……....142
8.7. Экспериментальное определение корреляционных функций,
спектральных плотностей и дисперсий случайных процессов………..146
8.8. Прохождение случайных воздействий через линейную систему………151
8.8.1. Интегральное уравнение связи между характеристиками
процессов на выходе и входе линейных систем….…………..……151
8.8.2. Спектральное уравнение связи между характеристиками
процессов на выходе и входе линейных систем….……….………156
8.9. Методы определения ошибок линейных САУ, обусловленных
стационарными случайными воздействиями…………………………….160
8.9.1. Эквивалентное представление стационарного случайного
процесса. Формирующий фильтр…………………………………..162
8.9.2. Расчет флуктуационных ошибок и ошибок от задающих
воздействий……………………………………………………..….163
8.9.3. Графоаналитический метод расчета ………………………………167
8.9.4. Оценка флуктуационных ошобок, обусловленных
широкополосными воздействиями……………………….………..168
8.9.5. Расчет дисперсии помехи с помощью корреляционной
функции………………………………………………………..… 171
8.8.6. Вычисление среднеквадратической ошибки
следящей сиситемы…………………………………………………174
Библиографический список…………………………………………….…..176
ВВЕДЕНИЕ
Лекция 1
План лекции:
1. Рассказать о значении автоматического управления и задачах курса.
2. История развития ТАУ.
3. Основы построения САУ. Принципы регулирования.
4. Рекомендуемая литература [1, 2, 8].
В.1. ЗНАЧЕНИЕ АВТОМАТИЧЕСКОГО УПРАВЛЕНИЯ
И ЗАДАЧИ КУРСА
Теория автоматического управления (ТАУ) – это наука, которая содержит общие принципы исследования и проектирования автоматических устройств – автоматических регуляторов, предназначенных для управления различными машинами или процессами без непосредственного участия человека. Автоматическое управление обладает целым рядом достоинств по сравнению с ручным. В частности, оно точнее и лишено субъективных ошибок, незаменимо в тех областях, в которых ручное управление невозможно или нецелесообразно. С помощью современной вычислительной техники осуществляется автоматизация всех основных видов производственной деятельности человека: 1) технологических процессов в самых различных отраслях, 2) проектных и конструкторских работ, 3) административно-организационной деятельности.
Без знания теории автоматического управления нельзя не только спроектировать, но и понять принцип работы современных приборов и систем.
Классические методы математики оказались недостаточными для решения практических задач теории управления. Поэтому при проектировании систем все чаще стали применяться методы теории автоматического управления.
Современная теория автоматического управления располагает мощными методами анализа и синтеза, позволяющими создавать высококачественные автоматические системы.
В.2. ИСТОРИЯ РАЗВИТИЯ ТАУ
Первые сведения об автоматах появились в начале нашей эры в работах Герона Александрийского «Пневматика» и «Механика», где были описаны автоматы: пневмоавтомат для открывания дверей храма при зажигании жертвенного огня, механический театр марионеток, прибор для измерения протяженности дорог, автомат для продажи священной воды. Идеи Герона значительно опередили свой век и не нашли промышленного применения в его эпоху.
В средние века начинает развиваться «андроидная», то есть человекоподобная автоматика. В XIII в. немецкий философ и алхимик Альберт фон Больштадт построил «железного человека» - робота для открывания и закрывания дверей.
Прекрасный «театр автоматов» был создан в XVIII в. русским механиком-самоучкой И.П. Кулибиным. Его «театр» помещен в «часах яичной формы», хранящейся в Государственном Эрмитаже.
На рубеже XVIII-XIX в. эпоху промышленного переворота в Европе, начинается новый этап развития автоматики, связанный с ее внедрением в промышленность. К первым промышленным автоматическим устройствам относятся регулятор уровня воды в котле паровой машины И.И. Ползунова (1765г.), регулятор скорости паровой машины Уатта (1784 г.).
По мере усложнения автоматических регуляторов встает вопрос о развитии их теории. Значительную роль в развитии теории автоматического управления сыграли работы выдающегося математика и механика П.Л. Чебышева, который в 1871 г. опубликовал работу «О центробежном уравнителе», где впервые поставлена задача о синтезе регулятора прямого действия.
Основоположником ТАУ считается профессор И.А. Вышнеградский. Идеи И.А. Вышнеградского получили свое дальнейшее развитие в работах словацкого инженера А. Стодола, который разработал теорию регуляторов с жесткой обратной связью, исследовал устойчивость схем непрямого регулирования.
Крупный вклад в теорию управления сделан Н.Е. Жуковским, автором труда «О прочности движения», и первого русского учебника «Теории регулирования хода машин».
В 1892г. вышла в свет работа А.М. Ляпунова «Общая задача об устойчивости движения», которая явилась существенной вехой в развитии теории устойчивости как линейных, так и нелинейных систем.
Значительный вклад в развитие теории автоматического управления внесли зарубежные ученые Раус, Гурвиц, Максвелл, Винер и другие.
К началу XX в. теория управления выходит из рамок прикладной механики и формируется в самостоятельную область науки.
В 1954 г. в СССР впервые в мире была введена в постоянную эксплуатацию полностью автоматизированная атомная электростанция, а в 1957 г. – выведен на орбиту искусственный спутник Земли. В 1961 г. был совершен первый в истории человечества космический полет, а в 1966 г. осуществлена мягкая посадка на Луну.
Большой вклад в развитие теории автоматического управления внесли советские ученые Е.Л. Николаи, И.Н. Вознесенский, В.С. Кулебакин и другие.
Исключительно важную роль в развитии теории автоматического управления сыграли работы А.В. Михайлова, которые были опубликованы в 1938 г. и открыли новый этап в теории управления. А.В. Михайлов показал целесообразность применения частотных методов и предложил новый критерий устойчивости. Ему также принадлежат идеи типизации динамических звеньев систем автоматического управления и структурных методов анализа.
Существенный вклад в направлении создания систем с заданным качеством регулирования внесли работы В.В. Солодовникова, А.А. Красовского, А.А. Фельдбаума, М.А. Айзермана и др.
Развитие нелинейной теории управления обязано выдающимся ученым Н.М. Крылову, Н.Н. Боголюбову, А.А. Андронову, А.А. Витте, С.Э. Хайкину, работы которых «Введение в нелинейную механику» и «Теория колебаний» получили мировую известность. Дальнейшее развитие нелинейная теория получила в работах Б.В. Булгакова, В.В. Петрова, Е.П. Попова, И.П. Пальтова, П.И. Кузнецова и др.
В 1950 г. В.С. Пугачев разработал математический аппарат для анализа динамических систем, находящихся под влиянием случайных воздействий, не связанный с предположением об их стационарности. Теоретические основы дискретных систем автоматического управления (САУ) развиты Я.З. Цыпкиным. Существенный вклад в развитие теории автоматического управления в нашей стране внесли Б.Н. Петров, А.С.Шаталов, А.Г. Ивахненко, А. М. Летов и др.
К основным научным результатам, достигнутым советским учеными в области линейной теории управления, следует отнести: принцип автономного регулирования, частотные методы анализа устойчивости, качества непрерывных и дискретных систем управления, интегральные оценки качества, принцип инвариантности, частотные методы синтеза систем при детерминированных и случайных воздействиях и многие другие. Значительное развитие получает и теория нелинейных автоматических систем. Здесь в первую очередь следует отметить: методы гармонической и статистической линеаризации, фазового пространства, точечных преобразований, развитие второго метода Ляпунова, принцип максимума и определение оптимальных законов управления, теорию синтеза нелинейных непрерывных и дискретных систем при регулярных и случайных возмущениях и т.д.
В.3. ОСНОВЫ ПОСТРОЕНИЯ САУ
Процесс поддержания или изменения по заданным условиям какой-либо величины в машинах или процессах, осуществляемый без непосредственного участия человека с помощью присоединяемых для этой цели автоматических регуляторов, называется автоматическим регулированием.
Машина, аппарат или иное устройство, к которому присоединяется автоматический регулятор, называется регулируемым объектом, а часть регулируемого объекта, на которую воздействует регулятор, - регулирующим органом. Величина, подлежащая изменению по заданному закону, называется регулируемой величиной.
Отклонением регулируемой величины в данный момент времени называется её отличие от некоторого фиксированного значения, принятого за начало отчета.
Предписанное значение регулируемой величины называют управляющей величиной.
Возмущающим называют всякое воздействие, которое стремится нарушить требуемую связь между управляющим воздействием и регулируемой величиной.
Совокупность автоматического регулятора и регулируемого объекта, взаимодействующих между собой, называется САУ.
В каждой системе автоматического управления можно указать вход (входную координату, входной сигнал) и выход (выходную координату, выходной сигнал).
Системы автоматического управления часто называют системами с обратной связью. Это объясняется тем, что во всякой системе автоматического управления должна иметься не только прямая связь между входом и выходом, при помощи которой производится управление регулируемой величиной, но и обратная связь между выходом и входом, служащая для сравнения обеих величин.
Сигнал, поступающий с выхода системы на ее вход, назовем сигналом главной обратной связи хос, а разность между входным сигналом хвх и сигналом главной обратной связи – сигналом ошибки
Δх = хвх- хос.
Главная обратная связь любой системы автоматического управления должна быть отрицательной, т. е. выходной сигнал должен поступать на вход системы с противоположным знаком. Для отрицательной обратной связи Δх=хвх-хос, для положительной Δх= хвх+хос.
Если входной сигнал и сигнал главной обратной связи имеют одну и туже физическую природу, то сигнал ошибки Δх можно считать ошибкой системы. Следует отметить еще одну характерную особенность систем автоматического управления, которая состоит в направленности их действия. Направленность действия заключается в том, что последующая часть системы, воспринимающая сигнал от предыдущей, оказывает ей пренебрежимо малое противодействие. На схемах направленность действия обозначается стрелками.
С учетом принятых обозначений и определений принципиальную схему САУ в общем виде можно представить так, как показано на рис. В.1. Пунктиром на схеме обозначен автоматический регулятор.
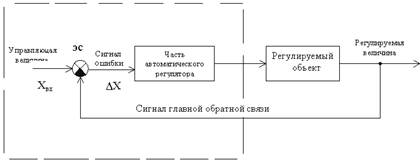
Рис. В.1
В основу построения автоматических регуляторов могут быть положены следующие принципы.
Принцип регулирования по отклонению предписывает закон изменения регулируемой величины, измеряет ее текущее значения, сравнивает предписанное (заданное) значение регулируемой величины с текущим, обнаруживает отклонение регулируемой величины от заданного значения и воздействует на регулируемый объект таким образом, чтобы устранить это отклонение.
Принцип регулирования по возмущению выявляет причины отклонения регулируемой величины от заданного значения и воздействует на регулируемый объект таким образом, чтобы устранить или компенсировать эти причины.
Регулирование по возмущению имеет ряд преимуществ. К ним относятся, в частности, как правило, больше быстродействие системы управления. Однако это регулирование имеет и недостатки. При регулировании по возмущению мы можем учесть действие лишь одного возмущения, а именно того, на которой регулирует автоматический регулятор.
Регулирование по отклонению получило на практике наибольшее применение, так как оно позволяет устранить отклонение регулируемой величины от заданного значения независимо от того, каким причинами это отклонение вызвано, т.е. устраняет влияние любых возмущений без их измерения.
Весьма эффективно применение комбинированного регулирования: по возмущению и по отклонению одновременно. Такие схемы объединяют преимущества обоих упомянутых принципов регулирования.
1. ОСНОВНЫЕ ПОНЯТИЯ И ОПРЕДЕЛЕНИЯ ТАУ
Лекция 2
План лекции:
1. Функциональная схема САУ.
2. Классификация САУ.
3. Примеры автоматических систем.
4. Рекомендуемая литература [1, 3, 7].
1.1. ФУНКЦИОНАЛЬНЫЕ ЭЛЕМЕНТЫ САУ
Любую САУ можно разбить на простые устройства направленного действия. Такие устройства в теории автоматического управления называют элементами. Причем, к основным элементам САУ относятся те элементы, без которых работа системы принципиально невозможна. Схемы, составленные из элементов, характеризующих функции, которые они призваны выполнять в общем контуре управления, называют функциональными схемами САУ.
Функциональные схемы не следует смешивать с блок-схемами, характеризующими систему по составу входящих в нее отдельных конструктивных блоков (блоков питания, распределительный щит и т.д.) Функциональная схема САУ показана на рис. 1.1.
На схеме приняты следующие обозначения:
ЗЭ - задающий элемент предназначен для выработки управляющей величины Х вх в соответствии с заданным законом управления;
ЭС - элемент сравнения предназначен для сравнения управляющей величины с сигналом главной обратной связи;
УЭ - управляющий элемент предназначен для формирования сигнала ошибки ΔХ по требуемому закону;
ЧЭ - чувствительный элемент предназначен для измерения регулируемой величины
ИЭ - исполнительный элемент непосредственно воздействует на регулируемый объект;
РО - регулируемый объект.
Кроме основных в систему могут входить дополнительные элементы - преобразующие, усилительные и корректирующие. Преобразующие элементы служат для преобразования физической величины.
Усилительные элементы служат для усиления сигналов по напряжению и мощности. Корректирующие элементы вводят в САУ для улучшения их динамических свойств.
Иногда в системе отсутствует исполнительный элемент. Такие системы называются системами прямого действия. Если же мощность на выходе управляющего элемента недостаточна, то в систему вводится исполнительный элемент. Такие системы называются системами непрямого действия.
|
|
|
| |||
| |||
|
|
|
|
|
 |  | ||||
|
Кроме главной обратной связи САУ могут иметь одну или несколько местных обратных связей, которые охватывают отдельные элемент системы, чаще всего, усилительные или исполнительные. Местные обратные связи вводятся для улучшения динамических свойств отдельных элементов системы. В подавляющем большинстве случаев местные обратные связи – отрицательные.
1.2. КЛАССИФИКАЦИЯ СИСТЕМ АВТОМАТИЧЕСКОГО
УПРАВЛЕНИЯ
Вследствие большого разнообразия САУ, различающихся функциональными возможностями, принципами построения и формой конструктивной реализации, дать законченную классификацию не представляется возможным. Поэтому, проведем классификацию САУ лишь по некоторым основным признакам.
1. По принципу регулирования САУ делятся на разомкнутые, замкнутые, комбинированные.
2. По характеру изменения управляющей величины (или по характеру изменения установившегося значения регулируемой величины) САУ делятся на системы стабилизации, следящие системы и системы программного регулирования.
В системах стабилизации управляющая величина должна быть постоянной или равной нулю. Регулируемая величина (напряжение, скорость, и т.п.) тоже должна быть постоянной, это условие вытекает из назначения системы. Однако под влиянием возмущений регулируемая величина может отклоняться от заданного постоянного значения. Это отклонение называется ошибкой стабилизации.
В следящих системах управляющая величина (следовательно, и регулируемая величина) является неизвестной (чаще всего случайной) функцией времени и пространства. Например, антенна радиолокатора должна поворачиваться, следуя маневру самолета, и следить за ним. При этом координаты самолета заранее неизвестны и могут изменяться по случайному закону.
В системах программного регулирования управляющая величина является заранее известной функцией времени или пространства, она вырабатывается программным устройством (или задающим элементом). Примером такого регулирования может служить автоматический полет беспилотного ЛА по заданной траектории.
3. В зависимости от отклонения регулируемой величины в установившемся режиме САУ делятся на статические и астатические.
САУ называется статической по отношению к постоянному возмущающему воздействию, если отклонение регулируемой величины, вызванное этим воздействием, с течением времени стремится к постоянной величине.
Астатическим регулированием называют такое регулирование, при котором в установившемся режиме при постоянной нагрузке поддерживается постоянное значения регулируемой величины, равное заданному значению, независимо от величины нагрузки. Установившаяся ошибка при астатическом регулировании равна нулю: практически вследствие неточности регулятора она возможна, но не будет зависеть от нагрузки.
4. По количеству обратных связей САУ можно разделить на одноконтурные и многоконтурные.
Одноконтурные системы имеют только лишь одну главную обратную связь. Многоконтурные системы, кроме главной обратной связи, имеют одну или несколько местных обратных связей, которые вводятся для улучшения динамики САУ.
5. По количеству регулируемых величин САУ делятся на одноканальные и многоканальные (одномерные и многомерные).
В одноканальных системах регулирование ведется только по одной выходной переменной.
В многоканальных системах регулирование осуществляется одновременно по нескольким выходным переменным.
6. По характеру сигналов САУ делятся на системы непрерывного действия, с гармоническим модулированным сигналом и дискретные.
Системой непрерывного действия называется такая система, в каждой из звеньев которой непрерывному изменению входной величины во времени соответствует непрерывное изменение выходной величины.
Системой дискретного действия (импульсной, релейной, цифровой) называется такая система, в которой хотя бы в одном звене при непрерывном изменении входной величины выходная величина изменяется не непрерывно.
7. В зависимости от динамических свойств САУ можно разделить на линейные и нелинейные.
Строго говоря, почти САУ нелинейные. Линейной системой называется такая система, динамика всех звеньев которой описывается линейными уравнениями (алгебраическими, дифференциальными или разностными). Для этого необходимо, прежде всего, чтобы статические характеристики всех звеньев системы были линейными, т. е. имели вид прямой линии.
Нелинейной системой называется такая система, в которой хотя бы в одном звене нарушается линейность статической характеристики или же имеет место любое другое нарушение линейности уравнений динамики звена (произведение переменных или их производных, корень, квадратный или более высокая степень переменной, либо другая нелинейная связь переменных и их производных).
В интересах простоты расчетов всегда желательно (там, где это допустимо) сводить задачу к такой форме, чтобы максимально использовать методы исследования линейных систем. Для этого системы стараются привести к линейным, и только для некоторых нелинейных звеньев учитывают их особые свойства.
Однако это вовсе не значит, что при проектировании новых автоматических систем нужно стремится к обыкновенным линейным системам, которые обладают ограниченными возможностями. Введение особых линейных и нелинейных звеньев может придать системе лучшие качества. Особенно богатыми возможностями обладают системы со специально вводимыми нелинейностями и дискретные системы, в том числе с цифровыми вычислительными устройствами, также самонастраивающиеся, экстремальные и самоорганизующиеся системы.
8. По характеру параметров САУ делят на стационарные, нестационарные и с распределительными параметрами. Если параметры не изменяются при действии системы, то система стационарная. Если изменением параметров во времени пренебречь нельзя, то система нестационарная. Если какое – либо звено описывается уравнением в частных производных (например, имеют место волновые процессы в трубопроводе или в электрической линии), то система будет с распределительными параметрами, в отличие от систем с сосредоточенными параметрами.
9. Все рассмотренные системы (вернее их математические модели) могут быть подразделены на детерминированные и статистические.
Математическая модель системы называется детерминированной, если приложенные к ней воздействия и характеризующие ее параметры предполагаются постоянными или вполне определенными функциями переменных состояния и времени.
Математическая модель системы называется статистической, если приложенные к ней воздействия и характеризующие ее параметры являются случайными функциями или случайными величинами.
1.3. ПРИМЕРЫ СИСТЕМ АВТОМАТИЧЕСКОГО УПРАВЛЕНИЯ
Пример 1. Система «Самолет – автопилот» (рис. 1.2). Здесь корпус самолета 1 является регулируемым объектом, гироскоп 2 с потенциометрической схемой служит измерительным устройством. Далее идут усилитель 3, двигатель 4 с редуктором 5 (рулевая машинка) и в качестве регулирующего органа - руль 6.
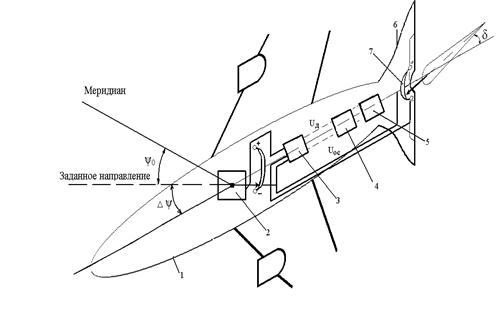
Рис. 1.2
Гироскоп сохраняет неизменное направление в пространстве. Поэтому при отклонении самолёта на угол ∆ ψ от заданного курса ψ 0 движок, связанный с гироскопом, смещается с нулевой точки. В результате на усилитель подаётся напряжение, пропорциональное углу отклонения ∆ ψ. Оно приводит в движение исполнительное устройство, состоящее из усилителя 3, рулевой колонки 4 и редуктора 5. При этом вследствие отклонения руля на угол δ самолёт возвратится в требуемое положение.
Очевидно, что если с помощью автопилота надо поддерживать неизменный курс ψ 0 или изменять по заданной программе, то данная система управления будет работать либо в режиме стабилизации постоянной величины, либо в режиме программного регулирования. Если же самолет надо наводить на какую-либо цель, визируемую дополнительным устройством (оптическим или радиолокационным) то данная система управления будет работать как следящая система.
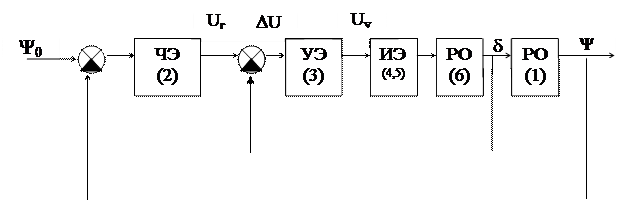
На рис.1.3 изображена функциональная схема рассмотренной системы, которая наглядно показывает взаимодействие элементов и позволяет оценить систему по различным признакам. Для улучшения устойчивости и качества стабилизации в систему вводятся различные корректирующие устройства и местные обратные связи 7.
| |||
| |||
. 1.4.
 |
Рис. 1.3
Пример 2. Система автоматического управления напряжением генератора постоянного тока. Принципиальная схема изображена на рис. 1.4.
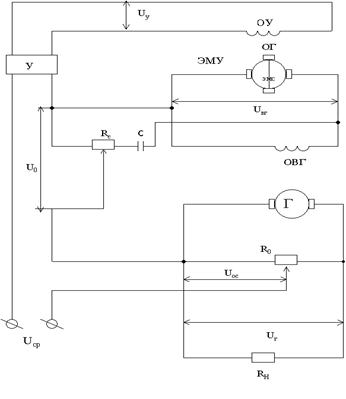
Рис.1.4
Система работает следующим образом. Напряжение обратной связи U oc, пропорциональное регулируемой величине – напряжению генератора U г, сопоставляется с напряжением сравнения. Разность U ср - U ос поступает на вход электронного усилителя У, питающего обмотку управления ОУ электромашинного усилителя (ЭМУ), являющегося возбудителем генератора Г. Для повышения динамической устойчивости системы в ней предусмотрена стабилизирующая местная обратная связь по напряжению ЭМУ, осуществляемая при помощи конденсатора С и резистора R с. Величина главной обратной связи устанавливается делителем R о.
При разделении системы автоматического управления на функциональные элементы (рис.1.5) генератор будем рассматривать как регулируемый объект РО. На него действует напряжение возбуждения U вг, являющееся регулирующим воздействием, и возмущающее воздействие – ток нагрузки I H.
Регулируемая величина U г преобразуется в напряжение U ос элементом главной обратной связи ГОС и сравнивается с напряжением U ср при помощи элемента сравнения ЭС, который в данном случае является электрическим соединением.
Стабилизирующий контур СR с представим как элемент местной обратной связи (MОC), входной величиной которого является напряжение усилителя U у, а входной – напряжение U о, вычитаемое из основного сигнала U ср - U ос.
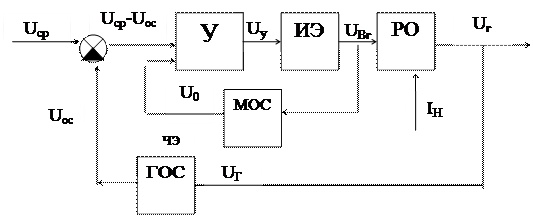
Рис. 1.5
Пример 3. Система автоматического регулирования скорости двигателя постоянного тока. Из рассмотрения принципиальной схемы системы управления (рис. 1.6.) видно, что скорость вращения двигателя преобразуется с помощью тахогенератора ТГ в напряжение обратной связи U ос, сравниваемое с задающим напряжением U з, изменяя которое можно задавать различную скорость двигателя. Разность U з– U ос суммируется с напряжением U о МОС, получаемым для повышения динамических свойств системы в стабилизирующем контуре R о С о, и подается на вход усилителя постоянного тока. При отсутствии сигнала на входе усилителя токи I у1 и I у2 равны между собой и результирующая МДС управления ЭМУ равна 0. Электромашинный усилитель нагружен на ОВ генератора, работающего на двигатель постоянного тока с независимым возбуждением по схеме генератор – двигатель.
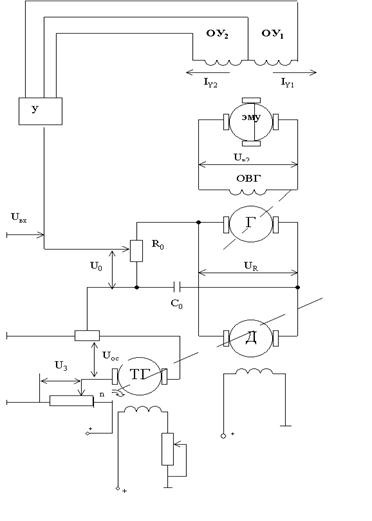
Рис.1.6
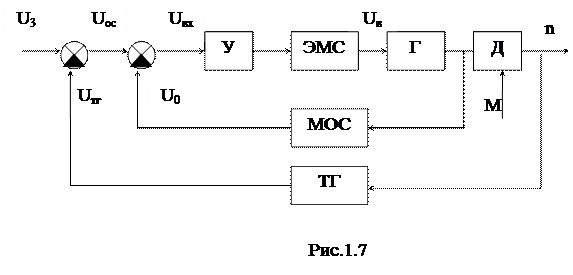
Функциональная схема САУ скорости двигателя постоянного тока представлена на рис. 1.7.
В соответствии со схемой рассмотренная система представляет собой двухконтурную, одноконтурную, астатическую систему стабилизации непрерывного действия.
Пример 4. Следящая система с асинхронным двухфазным двигателем. Принципиальная схема системы изображена на рис 1.8.
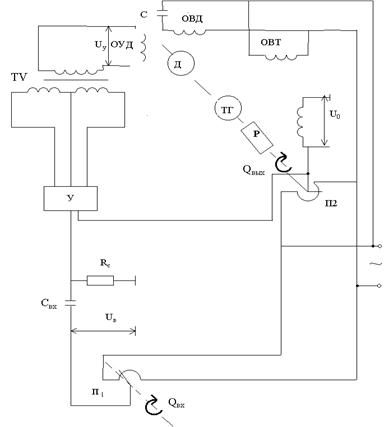
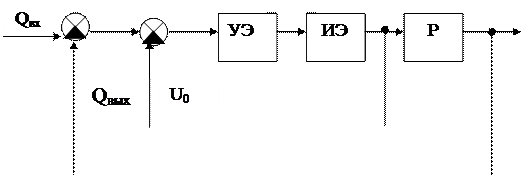
Рис. 1.8
|
|
|
 |
|
 | |||
 |
Рис. 1.9
2. МАТЕМАТИЧЕСКОЕ ОПИСАНИЕ САУ
Лекция 3
План лекции:
1. Виды воздействий. Управляющие и возмущающие воздействия.
2. Вынужденное движение и собственные колебания системы.
4. Рекомендуемая литература [1, 2, 4].
2.1. ВИДЫ ВОЗДЕЙСТВИЙ. УПРАВЛЯЮЩИЕ И ВОЗМУЩАЮЩИЕ ВОЗДЕЙСТВИЯ
Отклонение регулируемой величины САУ может быть вызвано влиянием управляющих и возмущающих воздействий. Управляющие воздействия всегда приложены к входу системы, т. е. к автоматическому регулятору.
Возмущающие воздействия могут быть приложены к любой точке САУ и делятся на нагрузку и помехи. Нагрузка – это воздействие, приложенное к регулируемому объекту при нормальной работе системы.
В реальных системах, как правило, и управляющие и возмущающие воздействия являются функциями времени (детерминированные) или задаются вероятностными характеристиками (случайные).
Чтобы упростить решение, реальные воздействия в теории автоматического управления заменяют идеальными или типовыми воздействиями.
1. Единичная скачкообразная функция (ступенчатое воздействие или единичный скачок). Это воздействие отражает мгновенное приложение или мгновенный сброс нагрузки или помехи. График единичной скачкообразной функции представлен на рис. 2.1, а. Аналитическая запись имеет следующий вид:
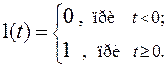
Ступенчатое воздействие с достаточной для практики точностью можно воспроизвести в лабораторных условиях с помощью низкочастотного генератора периодических колебаний или посредством механического воздействия на систему.
2. Единичная импульсная функция (единичный импульс, δ – функция). График δ – функции имеет вид, показанный на рис.2.1, б. Учитывая, что длительность функции h стремится к нулю, а высота 1 / h к бесконечности, δ – функцию можно представить себе в виде мгновенного импульса или удара.
Единичная скачкообразная и единичная импульсная функции связаны между собой следующим соотношением:
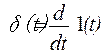. (2.1)
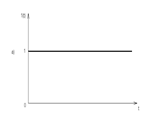
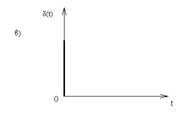
а б
Рис.2.1
Ступенчатое воздействие 1 (t) и δ (t)–функция применяются в основном при исследовании динамики САУ в переходном режиме, в частности, для построения графика переходного процесса и определения основных показателей качества.
3. Гармоническое воздействие. Имеет вид
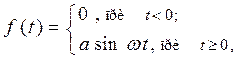(2.2)
или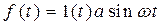 
,
где а и w - соответственно амплитуды и круговая частота гармонического воздействия. Применяются при исследовании ошибок САУ в установившихся режимах, при построении частотных характеристик и в других случаях.
4. Комплексное гармоническое воздействие. Имеет вид
f(t)= 1 (t) a (cos ωt + i sin ωt)= 1 (t)a eiωt . (2.3)
Воздействие отражает вибрации, действующие на систему, иногда применяется для аналитического определения частотных характеристик.
5. Воздействия,возрастающие во времени..
Пропорциональное времени:
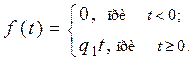(2.4)
Характеризует изменение управляющий величины с постоянной скоростью.
Пропорциональное квадрату времени:
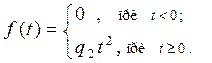(2.5)
Характеризует изменение управляющий величины с постоянным ускорением. Здесь q 1 и q 2 – постоянные коэффициенты.
Воздействия (2.4) и (2.5) применяются при исследовании следящих систем.
2.2. ВЫНУЖДЕННОЕ ДВИЖЕНИЕ И СОБСТВЕННЫЕ КОЛЕБАНИЯ СИСТЕМЫ. ПЕРЕХОДНЫЙ И УСТАНОВИВШИЙСЯ РЕЖИМЫ
В общем виде движение линейной САУ с постоянными параметрами описывается дифференциальным уравнением n -го порядка с постоянным коэффициентами
anx(n)+an-1x(n-1)+…+a1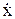
+a0x =bm
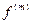(t)+ …+ b1
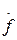(t)+b0
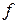(t). (2.6)
Допустим, что при t=0 переменные уравнения (2.6.) имеют следующие значения
x(0)=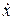
(0) = ….=x(n-1)(0)=x(n)(0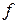)=0;
(0)=
; 
=
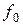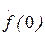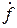0 ;……; 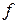(m-1)(0)= 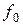(m-1); 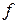(m)(0)= 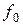(m).
При заданных начальных значениях переменных изображения отдельных слагаемых уравнения (2.6) можно записать в следующем виде:
a0 x(t)←: a0X(p); a1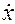
(t)←: a1pX(p);
………………….
an x (n) (t)←: anpnX(p);
b0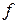(t)←: b0F(p); b1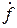(t)←: b1 (pF(p) - );
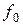b2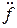
(t)←: b2(p2F(p) - p- 
);
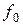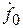……………………….. (2.7)
bm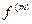
(t)←: bm (pmF(p) – p m-1
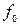– p m-2
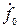- …- p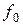(m-2)-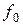(m-1) ).
С учетом (2.7) уравнение (2.6), записанное в операторном виде, можно представить следующим образом:
X(p) Д(р)= F(p) M(p) – MH(p), (2.8)
где Д(р)=anpn + an-1pn-1 +…+a1p +a0 - характеристический многочлен системы, представляющий собой изображение левой части уравнения (2.6) при нулевых начальных условиях;
M(p)=bmpm+bm-1pm-1+…+b1p+b0 – многочлен представляющий собой изображение правой части уравнения (2.6) при нулевых начальных условиях;
MH(p)=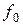(bmpm-1+bm-1pm-2+…+b2p+b1)+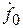(bmpm-2+b1p3+…+b3p+ +b2)+…+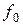(m-2)(bmp+bm-1)+ 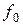(m-1)bm - многочлен, учитывающий начальные значения переменной f(t) и ее производных.
На основании (2.8) изображение выходной переменной принимает вид
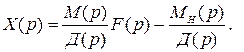(2.9)
Изображения F(p) внешних типовых воздействий представляют собой правильные рациональные дроби
.
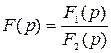Тогда, уравнение (2.9) можно представить следующим образом:
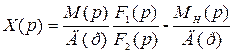(2.10)
Используя формулы обратного преобразования Лапласа, т.е. переходя от изображения Х(р) к оригиналу х (t), можно записать решение уравнения (2.6).
Рассмотрим случай, когда характеристическое уравнение Д (р)=0 и уравнение F2(p)= 0 не содержат нулевых и кратных корней.
Решение уравнения (2.6) с учетом (2.10) в этом случае можно представить в виде
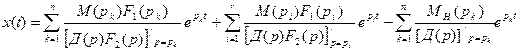, (2.11)
где pk – корни уравнения Д(р) = 0; pi - корни уравнения F2 (p) = 0;
n - порядок многочлена Д(р); r - порядок многочлена F2(р);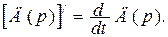 
Введем обозначения:
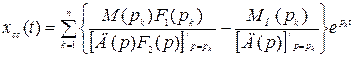, (2.12)
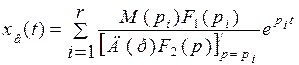. (2.13)
C учетом этого получим общее решение уравнения (2.6) в виде
х(t) = хcc(t) + хв (t), (2.14)
где х (t) - полное движение системы, вызванное внешним воздействием f (t);
х cc(t) – собственное движение системы; хв (t) – вынужденное движение системы.
Анализ полученного решения позволяет сделать следующие выводы:
а) полное движение САУ можно условно разделить на две составляющие:
собственное движение, не зависящее от внешнего воздействия f (t), и вынужденное движение, зависящее от него;
б) если характеристическое уравнение имеет хотя бы пару комплексных корней, то собственное движение будет колебательным;
в) если характеристическое уравнение имеет хотя бы один корень с положительной вещественной частью, то амплитуда собственных колебаний будет с течением времени неограниченно увеличиваться (система неустойчивая);
г) если характеристическое уравнение имеет все корни с отрицательными вещественными частями, то собственные колебания с течением времени будут затухать, т.е. если
pk= - δk ± iωk ,
то при t→ ∞ хcc(t)→ 0, а х(t)→ хв(t).
Таким образом, после затухания собственных колебаний полное движение системы стремится к вынужденному. Такое состояние системы называют установившемся.
Процесс перехода системы из одного установившегося состояния в другое называется переходным режимом. В переходном режиме система совершает как собственное, так и вынужденное движение. Длительность переходного режима определяется временем затухания собственных колебаний.
В общем случае начальные условия по всем переменным уравнения (2.6) отличны от нуля, т.е. при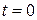 
: 
, 
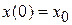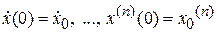, тогда в уравнении (2.8) появляется ещё один многочлен 
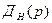, учитывающий начальные значения переменной 
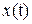и её производных, т.е. начальные условия самой системы:
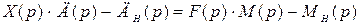, (2.15)
где
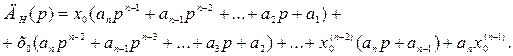
На основании (2.15) можно записать
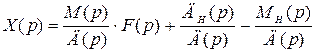. (2.16)
В соответствии с изображением (2.16) решение уравнения (2.6) будет иметь три составляющие:
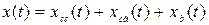, (2.17)
где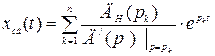 
. (2.18)
Выражение (2.18) характеризует свободное движение системы, полностью определяется корнями характеристического уравнения и от внешнего воздействия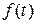 
не зависит.
Если характеристическое уравнение имеет все корни с отрицательными вещественными частями, то свободное движение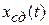 
системы с течением времени затухает, т.е. если 
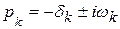, то 
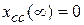и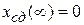 
, и полное движение САУ 
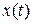стремится к вынужденному 
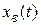. Наступает установившийся режим. В частном случае установившемуся режиму САУ соответствует покой или равновесие.
2.3. ПЕРЕДАТОЧНЫЕ ФУНКЦИИ
Передаточной функцией элемента или системы называют отношение преобразования Лапласа выходной величины к преобразованию Лапласа входной величины элемента или системы при нулевых начальных условиях.
Для определения аналитического выражения передаточной функции в общем виде достаточно, таким образом, записать уравнение (2.6) в изображениях по Лапласу при нулевых начальных условиях по всем переменным и записать отношение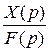 
.
Если при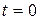 
: 
, 
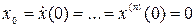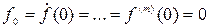, то на основании (2.6) можно записать
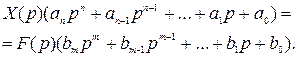(2.19)
В соответствии с определением выражение для передаточной функции САУ в общем виде можно записать из уравнения (2.19):
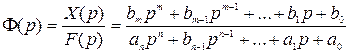. (2.20)
Как видно из уравнения (2.20) передаточная функция представляет собой правильную рациональную дробь. Знаменатель передаточной функции
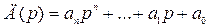
представляет собой характеристический многочлен системы, а числитель
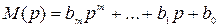
является изображением правой части уравнения (2.6) при нулевых начальных условиях.
В САУ степень знаменателя в выражении (2.20) всегда больше или равна степени числителя, т.е.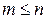 
.
В ТАУ также используют передаточную функцию ошибки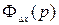 
, которую определяют как отношение преобразования Лапласа сигнала ошибки 
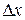к преобразованию Лапласа входной величины 
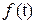при нулевых начальных условиях, т.е.
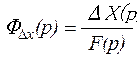. (2.21)
Используя передаточные функции (2.20) и (2.21), можно определить изображения регулируемой величины и ошибки САУ по формулам:
; 
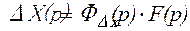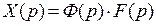. (2.22)
Лекция 4
План лекции:
1. Переходная характеристика и весовая функция системы.
2. Типовые звенья САУ.
3. Неустойчивые и неминимально–фазовые звенья.
4. Рекомендуемая литература [1, 4, 7].
2.4. ПЕРЕХОДНАЯ ХАРАКТЕРИСТИКА И ВЕСОВАЯ ФУНКЦИЯ
Для исследования динамики САУ в переходном режиме используются переходные характеристики и весовые функции.
Переходной характеристикой системы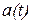 
называют её реакцию (изменение во времени выходной величины) на единичное скачкообразное воздействие 
.
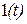Весовой функцией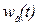 
(функцией веса) системы называют её реакцию на единичное импульсное воздействие 
.
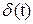В соответствии с этими определениями можно утверждать, что они связаны между собой так же, как единичное ступенчатое воздействие с дельта-функцией, т. е.
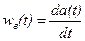; (2.23)
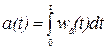. (2.24)
Зная переходную характеристику или весовую функцию, можно определить реакцию системы или звена на произвольное входное воздействие при нулевых начальных условиях.
2.5. ТИПОВЫЕ ЗВЕНЬЯ СИСТЕМ АВТОМАТИЧЕСКОГО
УПРАВЛЕНИЯ
Деление САУ на функциональные элементы не отражает динамические свойства ни системы, ни элементов. Поэтому, САУ "разбивают" на отдельные устройства в зависимости от динамических свойств этих устройств, которые называют динамическими звеньями. Типовым динамическим звеном называет звено, для которого связь между входным и выходным сигналами описывается дифференциальным уравнением не выше второго порядка. Рассмотрим наиболее часто встречающиеся типовые звенья.
1. Усилительное звено (безынерционное) характеризуется тем, что выходной сигнал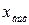 
пропорционален входному 
:
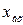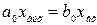, или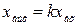 
,
где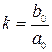 
- коэффициент передачи усилительного звена (если размерности коэффициентов 
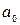и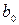 
совпадают, то называют 
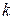коэффициентом усиления).
На основании (2.25) при нулевых начальных условиях имеем
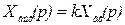, (2.26)
или
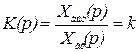, (2.27)
где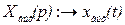 
; 
.
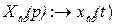Для определения переходной характеристики 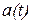необходимо определить реакцию звена 
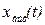на единичное скачкообразное воздействи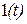е т.е,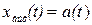 
, если 
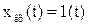. В соответствии с этим
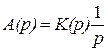, (2.28)
где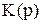 
- передаточная функция звена.
; 
.
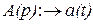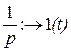Для определения весовой функции 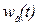необходимо определить реакцию звена 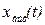на единичное импульсное воздействие, 
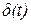т.е.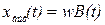 
, если 
.
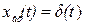В соответствии с этим
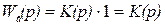, (2.29)
где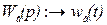 
; 
.
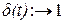Выражения (2.28) и (2.29) позволяют определить изображения переходной характеристики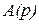 
и весовой функции 
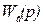по передаточной функции 
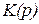звена. Так для усилительного звена на основании (2.28) и (2.29) с учётом (2.27) можно записать
; 
,
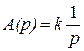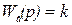т. е.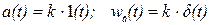 
.
Изложенная методика может быть применена для определения переходных характеристик и весовых функций всех типовых звеньев.
2. Интегрирующее звено характеризуется уравнением
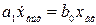или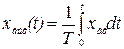 
, (2.31)
где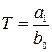 
- постоянная времени интегрирующего звена.
Соответствующая (2.31) передаточная функция интегрирующего звена имеет вид
.
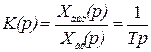В соответствии с (2.28) и (2.29)
; 
,
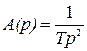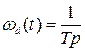т. е.
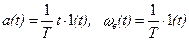. (2.33)
3. Дифференцирующее звено описывается уравнением
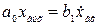или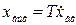 
, (2.34)
где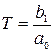 
.
На основании (2.34) имеем
;
; 
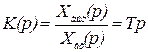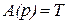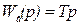; (2.35)
т. е.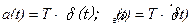 
. (2.36)
4. Апериодическое (инерционное) звено. Уравнение этого звена имеет вид
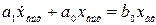, или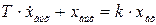 
,
где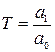 
; 
.
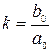Соответственно передаточная функция определяется выражением
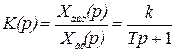; (2.37)
На основании (2.37) имеем:
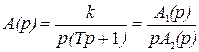; (2.38)
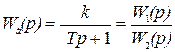; (2.39)
Применяя формулу обратного преобразования Лапласа, будем иметь
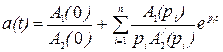, (2.40)
где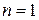 
; 
; 
; 
; 
; 
.
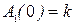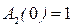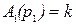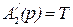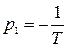Тогда (2.40) примет вид
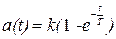. (2.41)
Выражение для весовой функции на основании (2.39) имеет вид
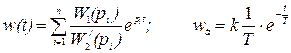. (2.42)
5. Колебательное звено. Уравнение для этого звена имеет вид
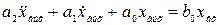, или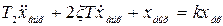 
, (2.43)
где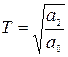 
; ; 
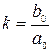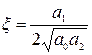- коэффициент относительного демпфирования, причём для колебательного звена 
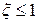. Передаточная функция колебательного звена, соответствующая уравнению (2.43), имеет вид
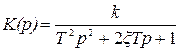. (2.44)
Если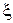 
окажется больше единицы, то это звено называется апериодическим звеном второго порядка, а его передаточная функция записывается в виде
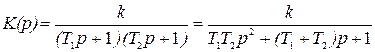, (2.45)
где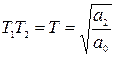 
; 
.
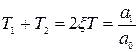На основании (2.44) имеем:
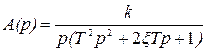; (2.46)
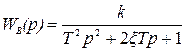. (2.47)
Применяя формулы обратного преобразования Лапласа, можно показать, что выражения для переходной характеристики и весовой функции, соответствующие (2.46) и (2.47), имеют вид:
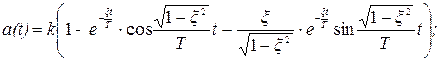(2.48)
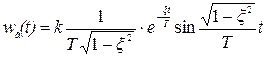. (2.49)
Графики переходных характер
