2014-02-02
2236
Знакопеременные ряды. Теорема об абсолютной сходимости
Теорема 8.8. Числовой ряд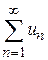 
сходится, если сходится ряд, составленный из абсолютных величин его членов 
.
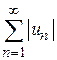Д о к а з а т е л ь с т в о. Пусть ряд 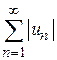сходится. Тогда по свойству 1 сходящихся рядов также сходится ряд 
.
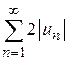Так как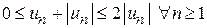 
, то по первому признаку сравнения рядов (теорема 8.2) также сходится ряд 
. На основании свойства 2 сходящихся рядов сходится разность двух рядов
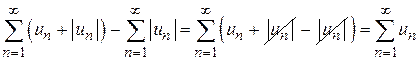, т. е. исходный ряд.
Ряд называется абсолютно сходящимся, если он сходится и сходится ряд, составленный из абсолютных величин его членов.
Ряд называется условно сходящимся, если он сходится, а ряд, составленный из абсолютных величин его членов, расходится.
Пример 8.19. Исследовать сходимость ряда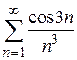 
.
Так как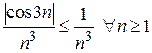 
и ряд 
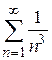сходится как обобщенно гармонический ряд 
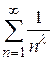при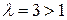 
, то по теореме 8.2 сравнения рядов сходится ряд 
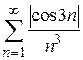, а по теореме об абсолютной сходимости сходится также ряд 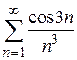. Следовательно, исходный ряд сходится; причем абсолютно.
Пример 8.20. Исследовать на абсолютную сходимость ряд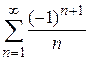 
.
Ранее было показано, что данный знакочередующийся ряд сходится (пример 8.15). Ряд, составленный из абсолютных величин данного ряда, является гармоническим, который, как известно, расходится. Это означает, что исходный ряд сходится условно.
