Теорема Абеля о виде области сходимости степенного ряда

В общем случае степенной ряд имеет вид

,

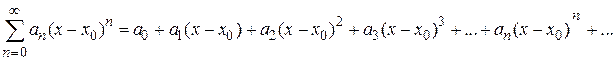где 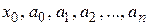- постоянные величины, х – переменная величина.

В частном случае при 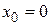ряд имеет вид

.

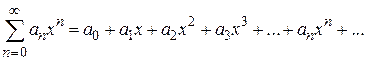При конкретных значениях х ряд является числовым и можно исследовать его сходимость и находить область его сходимости.

Теорема 9.2. (Теорема Абеля). 1. Если степенной ряд 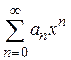сходится при некотором значении 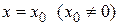, то он сходится также при любых значениях х, для которых 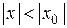. 2. Если степенной ряд расходится при 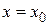, то он также расходится при любых значениях х, для которых .

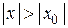Д ок а з а т е л ь с т в о. 1. Пусть степенной ряд 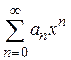сходится при 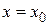, т. е. ряд 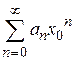является сходящимся. Тогда его члены 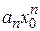ограничены при любых значениях степени n, т. е. , где .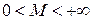

Составим ряд из абсолютных величин членов исходного ряда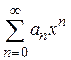

.

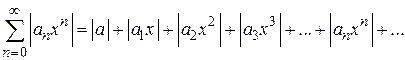Покажем, что этот ряд сходится, если 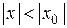. Преобразуем все его члены следующим образом: 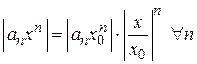, а также учтем, что при 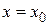все его члены ограничены величиной М. Тогда можно записать неравенство

£

.

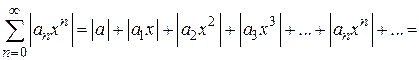
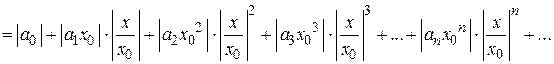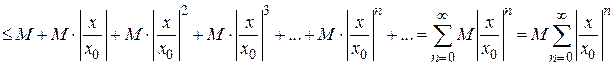При 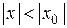ряд 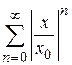представляет бесконечную убывающую геометрическую прогрессию со знаменателем 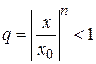, которая сходится. Следовательно, сходится ряд .

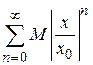Ввиду того, что члены ряда 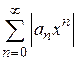меньше соответствующих членов сходящегося ряда 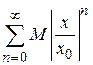, по теореме 8.2 этот ряд сходится.

В соответствии с теоремой 8.8 об абсолютной сходимости ряда сходится также исходный ряд 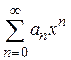, причем абсолютно.

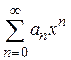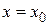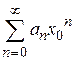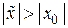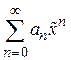2. Пусть теперь ряд расходится при , т. е. расходится ряд . Докажем от противного, что при ряд расходится. Предположим, что при 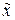исходный ряд сходится. Тогда по доказанному в первой части настоящей теоремы он должен сходится также и при меньших по модулю значениях х, т. е. при 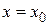. В этом и состоит противоречие.

Теорема Абеля является теоремой о виде области сходимости степенного ряда, так как если ряд сходится при 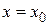, то он сходится и при 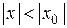, т. е. при . Следовательно, область сходимости симметрична относительно начала координат (рис. 85).

Рис. 85