2014-02-02
1993
Теорема 8.5. Если для знакоположительного ряда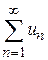 
существует предел
, то: 1) если r < 1, то ряд сходится; 2) если r > 1, то ряд расходится; 3) если r = 1, то данный признак не позволяет решить вопрос о сходимости ряда (ряд может как сходиться, так и расходиться).
Д о к а з а т е л ь с т в о. 1. Пусть 
. Если r < 1, то всегда найдется число q, удовлетворяющее неравенству r < q < 1. Тогда по определению предела существует такое число N, что если n > N, то 
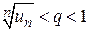. Возведем это неравенство в n -ю степень, имеем 
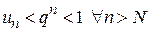. При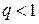 
геометрическая прогрессия 
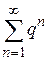сходится. По теореме 8.2 (первый признак сравнения) ряд 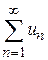сходится.
2. Пусть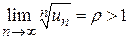 
. Если r > 1, то всегда найдется число q, удовлетворяющее неравенству 1 < q < r. Тогда существует такое число N, что если n > N, то 
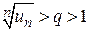. Возведем это неравенство в n -ю степень, имеем 
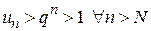. При 
геометрическая прогрессия 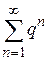расходится. По теореме 8.2 (первый признак сравнения) ряд 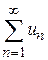расходится.
Пример 8. 12. Исследовать сходимость ряда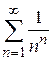 
.
Находим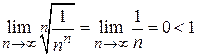 
. Ряд сходится.
