Ряды Тейлора и Маклорена

Функция разлагается в степенной ряд 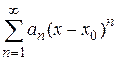в области G, если он составлен для этой функции и сходится к ней.

Пусть степенной ряд

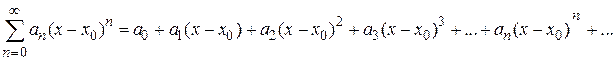
Равномерно сходится к функции , т. е.

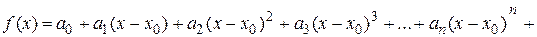
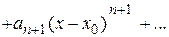
Тогда его можно почленно дифференцировать.

Найдем производные этого ряда.

;

;

;

………………………………………………………………………………………

……………………………………………………………………………………………………

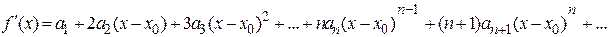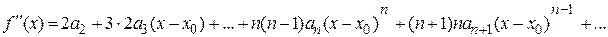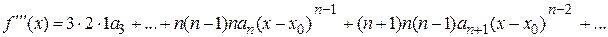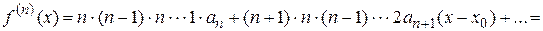
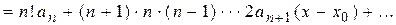
Подставим значение 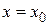в эти соотношения

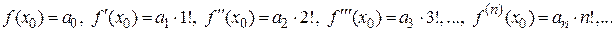,получим формулы для нахождения коэффициентов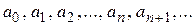

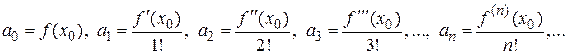
Следовательно,

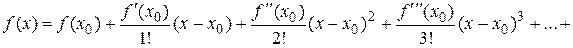
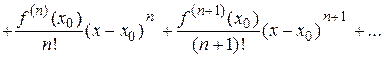
Данный ряд называется рядом Тейлора.

При 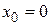данный ряд имеет вид

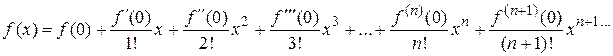
и называется рядом Маклорена.

Разложения функций по данным формулам справедливы только в области сходимости этих рядов.

Ранее были получены формулы Тейлора и Маклорена (Математический анализ. Часть 1. Дифференциальное исчисление).

В формуле Тейлора

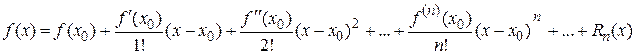
остаточный член можно рассматривать как остаточный член ряда Тейлора. В форме Лагранжа он имеет вид

,

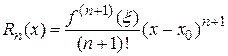где 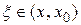или .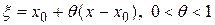

Также для ряда Маклорена

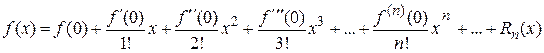
остаточный член в форме Лагранжа имеет вид

.

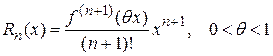Теорема 9.2. Для того чтобы степенной ряд 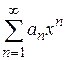сходился к функции , для которой он составлен, необходимо и достаточно, чтобы остаточный член ряда стремился к нулю при неограниченном увеличении его номера n, т. е. .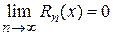

Д о к а з а т е л ь с т в о.

Необходимость. Пусть ряд 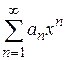сходится к функции , т. е.

.

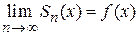Так как 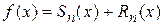, то

.

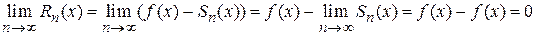Достаточность. Пусть .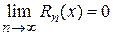

Тогда

,

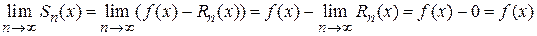т. е. ряд сходится.