Интеграл Коши - Лагранжа

Потенциальные течения идеальной жидкости.

Для потенциальных течений идеальной жидкости, как установившихся, так и неустановившихся, может быть получен интеграл Коши – Лагранжа.

Рассмотрим движение идеальной жидкости, определенное по отношению к некоторой системе отсчета, и запишем уравнение движения в форме Громеки – Лемба, (7.12). Предположим, что:

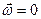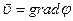- движение потенциально, т.е. и , где 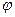– потенциал скоростей;

- имеет место баротропия, 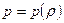, а значит, можно ввести единую для всего потока функцию давления .

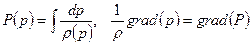При этих предположениях уравнение Громеки – Лемба запишется в виде

.

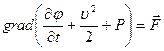Отсюда видно, что массовые силы в этом случае должны обладать потенциалом 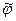. Тогда уравнение (7.12) приобретает вид

.

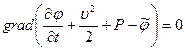Отсюда следует, что

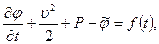(7.35)

где 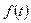– некоторая произвольная функция времени .

Соотношение (7.35), выполняющееся во всех точках области потенциального движения жидкости или газа, называется интегралом Коши – Лагранжа.

Для определения функции 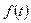достаточно знать левую часть интеграла как функцию времени в какой-либо одной точке потока, например, в некоторой точке, принадлежащей границе потока. В случае же безграничной жидкости функцию 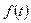можно определить по заданным значениям потенциала 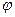и других характеристик на бесконечности. Т.к. потенциал 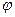определен с точностью до произвольной функции времени, вместо потенциала 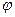можно ввести потенциал 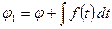(введение в потенциал 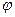добавочного члена не влияет на поле скоростей, т.к. 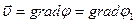). Заменяя в (7.35) 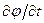через 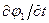получим, что функция 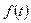в интеграле Коши – Лагранжа равна нулю. В этом случае потенциал 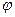определяется с точностью до аддитивной постоянной по времени и по координатам.

В частном случае, когда потенциальное движение жидкости установившееся, интеграл Коши – Лагранжа совпадает с интегралом Бернулли.

Интеграл Коши – Лагранжа (7.35) был получен в предположении, сто потенциал скоростей 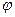представлен как функция времени и координат системы отсчета, по отношению к которой рассматривается движение. Однако для описания движения относительно некоторой системы отсчета можно пользоваться другой, подвижной по отношению к системе отсчета, системой координат (например, жестко скрепленной с телом, движущимся в жидкости).

Формулы преобразования координат

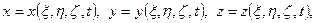
где 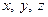– декартовы координаты относительно системы отсчета, а 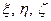– координаты точек относительно подвижной системы. Потенциал скоростей можно представить как функцию 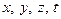или как функцию :

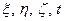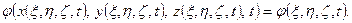
Интеграл Коши – Лагранжа (7.35) является следствием уравнений импульса, поэтому в него входит частная производная потенциала 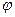по времени , вычисленная в той системе координат, относительно которой рассматривается движение. Заметим, что

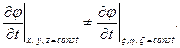
Установим связь между этими производными. Имеем

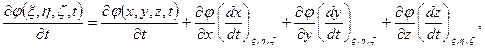
причем

а

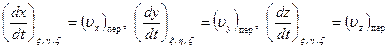
являются компонентами в системе отсчета 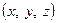скорости движения точки, жестко связанной с подвижной системой, т.е. переносной скорости 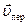. Поэтому

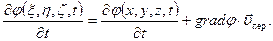
Скалярное произведение 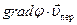является инвариантной величиной и может быть записано как через компоненты векторов в системе 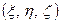, так и через компоненты в системе 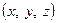. Если потенциал 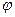определяется как функция 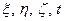, то интеграл Коши – Лагранжа (7.35) принимает вид

.

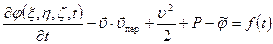Если предположить, что подвижная система координат движется как абсолютно твердое тело, то, как известно,

,

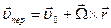где – скорость начала координат подвижной системы относительно системы 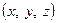, 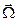– мгновенная угловая скорость вращения подвижной системы и 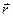– радиус-вектор рассматриваемой точки относительно подвижной системы координат. В частном случае, когда подвижная система движется поступательно с постоянной скоростью 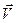вдоль оси 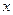, интеграл Коши – Лагранжа для несжимаемой жидкости, когда 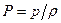, представится в виде

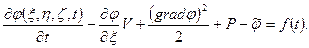(7.35’)

Основными уравнениями потенциальных течений идеальной жидкости (газа) в случае баротропных процессов 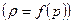являются уравнение неразрывности и интеграл Коши – Лагранжа:

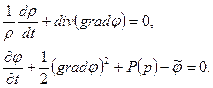(7.36)

Для дифференциала функции давления 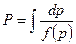имеем

,

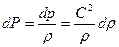где . Следовательно,

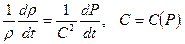
Систему уравнений (7.36) можно переписать в виде

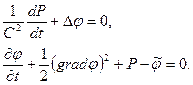(7.37)

Неизвестными в этой системе являются функция давления 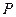и потенциал скоростей 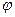. В общем случае эту нелинейную систему дифференциальных уравнений проинтегрировать трудно, однако для некоторых важных классов движения методы решения системы уравнений (7.37) подробно изучены. К таким классам потенциальных движений жидкости относятся следующие.

Потенциальные течения несжимаемой жидкости. В этом случае 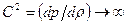и первое уравнение системы (7.37) сводится к уравнению Лапласа 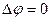. Второе уравнение системы служит в этом случае для определения давления. В такой постановке рассматриваются такие задачи, как задачи о движении воды, возникшем при перемещении в ней твердых тел, задачи о волнах на поверхности воды, задачи о струйных течениях воды, и другие.

Движения сжимаемой жидкости или газа, представляющие собой малые возмущения некоторого известного состояния равновесия или движения. Такие движения изучаются, например, в акустике (задачи о распространении звуковых волн). При решении задач о движении среды с малыми возмущениями предполагают, что скорость, плотность, давление и их производные по координатам и времени представляют собой известные функции плюс неизвестные малые добавки (возмущения). Пренебрегая малыми величинами порядка выше, чем первый, получаем линейную систему уравнений. Считая, что движение представляет собой малое возмущение около состояния покоя, систему уравнений (7.37) с точностью до малых первого порядка, можно записать в виде

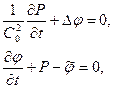
где 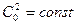– значение производной 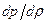, вычисленное для невозмущенного состояния покоя. Из этих двух уравнений можно получить одно уравнение, которое, если потенциал массовых сил не зависит от времени, имеет вид

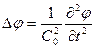. (7.38)

Это линейное уравнение называется волновым уравнением.

Установившиеся движения сжимаемой жидкости. Наибольшее развитие в данном случае получила теория плоскопараллельных течений, когда искомые функции зависят лишь от двух пространственных переменных. Уравнения движения в этом случае специальной заменой переменных и искомых функций удается преобразовать к линейным. Такое преобразование было предложено С.А. Чаплыгиным в 1902 г. в его работе “О газовых струях”.

Одномерные неустановившиеся течения. В этом случае все параметры движения зависят только от одной пространственной координаты и времени. Система уравнений в этом случае нелинейна.