Совершенного газа

Интеграл Бернулли для адиабатических течений

Рассмотрим обратимые адиабатические течения совершенного газа. Тогда, на основе (4.38),

,

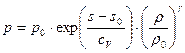где для частицы газа. Для функции давления 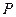вдоль линии тока имеем

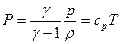. (7.24)

В самом деле, опуская постоянные интегрирования:

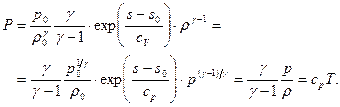
Величина 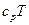для совершенного газа равна внутреннему теплосодержанию (энтальпии) 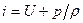. Тогда для установившихся адиабатических движений произвольных двухпараметрических идеальных сред, т.к., согласно уравнению притока тепла, вдоль линии тока

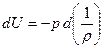, т.е. ,

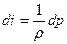то функция давления представляет собой энтальпию.

На основе (7.24), интеграл Бернулли вдоль линии тока для адиабатических движений при пренебрежении массовыми силами,

,

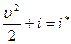или для совершенного газа,

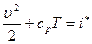. (7.25)

Из (7.24) и (7.25) видно, что давление, плотность и температура с ростом скорости вдоль линии тока падают.

Очевидно, что самая высокая температура на линии тока будет там, где 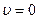. Пусть она равна 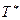. Тогда постоянную интеграла Бернулли можно записать как , где 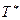– температура торможения, а 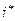– полное теплосодержание.

Аналогично, в точке 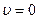давление и плотность имеют значения, максимально возможные на линии тока. Тогда можно также записать:

. (7.26)

При заданном значении полного теплосодержания 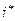температура торможения полностью определяется через 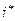. Давление и плотность торможения зависят на линии тока не только от 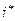, но и от значения энтропии 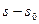. Если энтропия возрастает за счет пересечения частицами скачков уплотнения, то 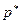и уменьшаются.

Из интеграла Бернулли видно, что в точке 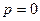скорость газа имеет максимальное значение 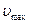. Тогда постоянная в интеграле Бернулли будет равна

.

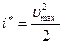Скорость 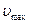можно считать скоростью истечения газа из баллона в пустоту, где 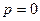, , 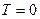. Учитывая, что, с одной стороны, , а с другой стороны, 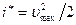, то

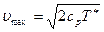, (7.27)

т.е. 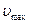зависит только от температуры торможения. При установившемся движении скорость газа не может быть больше 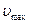, определяемой по (7.27), при неустановившихся адиабатических движениях в потоке могут получаться скорости, температуры, давления и плотности, большие чем , , , .

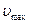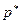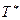Обозначим 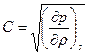– скорость звука. Для совершенного газа

.

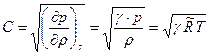Тогда интеграл Бернулли можно записать в виде

. (7.28)

Отсюда видно, что при изменении скорости частиц 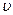скорость звука вдоль линии тока меняется. Если скорость вдоль линии тока растет до 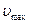, то скорость звука убывает до нуля.

В точке торможения 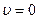, значит, в этой точке скорость звука максимальна (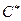). Тогда 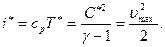Поэтому 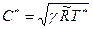и

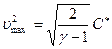. (7.29)

Значение скорости частицы газа, равное местной скорости звука, называется критической скоростью и обозначается через 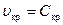. Из интеграла Бернулли при 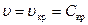имеем

,

откуда

. (7.30)

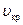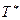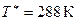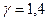Значение зависит только от температуры торможения . Например, при и имеем

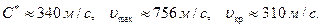
Течение газа называется дозвуковым, если скорости движения частиц меньше местной скорости звука 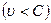, и сверхзвуковой, если .

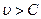Отношение скорости движения частиц к местной скорости звука называется числом Маха:

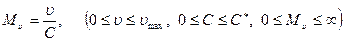
Наряду с числом Маха 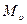используют отношение скорости движения частиц к критической скорости

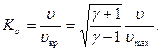
Величина 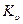называется коэффициентом скорости.

Рассмотрим зависимость скорости от значений параметров торможения и давления вдоль линии тока. Для этого возьмем интеграл Бернулли в виде

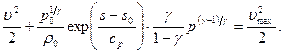
Поделим первое слагаемое на величину 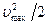, а второе – на равную ей величину

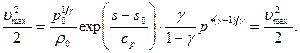
Получим:

,

откуда

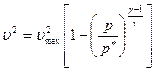, (7.31)

или

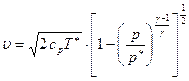. (7.32)

Формула (7.32) называется формулой Сен-Венана – Вентцеля. Она может быть использована для определения скорости установившегося истечения газа через насадок из сосуда, в котором 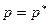, 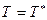в пространство с давлением 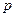(однако чтобы действительно иметь на выходе из насадка давление 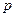, необходимо сделать насадок специальным образом).

Аналогичным образом, на основе (7.24), интеграл Бернулли можно разрешить относительно давления, плотности и температуры:

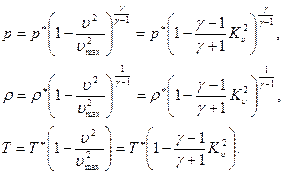(7.33)

Запишем аналогичные соотношения с использованием числа Маха. Перепишем уравнение Бернулли в виде

.

Разделив обе части этого равенства на , получим

.

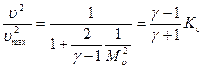Формулы (7.33) можно переписать в виде

(7.34)

С ростом скорости потока температура в потоке падает. Если же в поток газа поместить неподвижное твердое тело, то оно будет нагреваться.

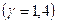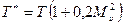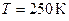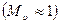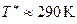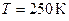Так, для воздуха температура вблизи критической точки тела будет равна . Если температура потока вдали от тела , то при скорости потока порядка скорости звука , . При и имеем 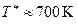, а при 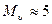имеем .

С другой стороны, при засасывании покоящегося воздуха с 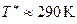в области больших скоростей можно получить очень малые температуры 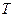, например, при 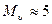будет происходить такое охлаждение, что воздух в потоке начнет конденсироваться в жидкость.