Пусть в точке пространства с координатами x, y, z в момент времени t происходит некоторое физическое явление (событие). Пусть в другой точке x1, y1, z1 в момент времени t, происходит другое событие, тогда по определению интервалом между двумя событиями называется величина равная: S=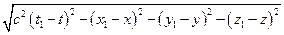 (9). Преобразуем (9), чтобы узнать чему оно равно в системе К’, пользуясь формулами (II). c2(t1-t)2=1/(1-V2/c2){c2(t1’-t’)2+2V(x1’-x’)(t1’-t’)+V2/c2(x1’-x’)2}, (x1-x)2=(x1’-x’)2+V2(t1’-t’)2+2V(x1’-x’)(t1’-t’), (y1-y)2=(y1’-y’)2, (z1-z)2=(z1’-z’)2, c2(t1-t)2-(x1-x)2=1/(1-V2/c2){ c2(t1’-t’)2+2V(x1’-x’)(t1’-t’)+V2/c2(x1’-x’)2-(x1’-x’)2-V2(t1’-t’)-2V(x1’-x’)(t1’-t’)}=1/(1-V2/c2){ (t1’-t’)2(c2-V2)+ (x1’-x’)2(1-V2/c2)}= 1/(1-V2/c2){c2(t1’-t’)2(1-V2/c2)-(x1’-x’)2(1-V2/c2)}=c2(t1’-t’)2-(x1’-x’)2, S2=c2(t1-t)2-(x1-x)2-(y1-y)2-(z1-z)2=c2(t1’-t’)2-(x1’-x’)2-(y1’-y’)2-(z1’-z’)2=S’2 (10). S=S’=invar (11).
(9). Преобразуем (9), чтобы узнать чему оно равно в системе К’, пользуясь формулами (II). c2(t1-t)2=1/(1-V2/c2){c2(t1’-t’)2+2V(x1’-x’)(t1’-t’)+V2/c2(x1’-x’)2}, (x1-x)2=(x1’-x’)2+V2(t1’-t’)2+2V(x1’-x’)(t1’-t’), (y1-y)2=(y1’-y’)2, (z1-z)2=(z1’-z’)2, c2(t1-t)2-(x1-x)2=1/(1-V2/c2){ c2(t1’-t’)2+2V(x1’-x’)(t1’-t’)+V2/c2(x1’-x’)2-(x1’-x’)2-V2(t1’-t’)-2V(x1’-x’)(t1’-t’)}=1/(1-V2/c2){ (t1’-t’)2(c2-V2)+ (x1’-x’)2(1-V2/c2)}= 1/(1-V2/c2){c2(t1’-t’)2(1-V2/c2)-(x1’-x’)2(1-V2/c2)}=c2(t1’-t’)2-(x1’-x’)2, S2=c2(t1-t)2-(x1-x)2-(y1-y)2-(z1-z)2=c2(t1’-t’)2-(x1’-x’)2-(y1’-y’)2-(z1’-z’)2=S’2 (10). S=S’=invar (11).
▼ Мы показали, что интервал между двумя событиями является инвариантным. Мы рассматриваем бесконечно малые расстояния и интервалы между двумя событиями dx=(x1-x), dt=(t1-t), dS=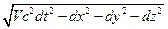 (12). Пусть дана инерциальная система отсчета К’, в некоторой точке x’, y’, z’ происходит два события во время dt0-измеряется часами, покоящимися в К’. Время dt0 есть собственное время, прошедшее между двумя событиями. Найдем интервал между двумя событиями. dS=
(12). Пусть дана инерциальная система отсчета К’, в некоторой точке x’, y’, z’ происходит два события во время dt0-измеряется часами, покоящимися в К’. Время dt0 есть собственное время, прошедшее между двумя событиями. Найдем интервал между двумя событиями. dS=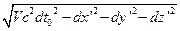 =cdt0, dt0=
=cdt0, dt0=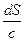 (13)-связь интервала и времени. Подставим в (13) dS из формулы (12): dt0=
(13)-связь интервала и времени. Подставим в (13) dS из формулы (12): dt0=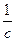
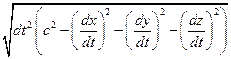
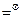
 =(
=(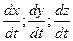 ) (14)
) (14)
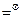 dt
dt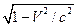 . dt0=dt
. dt0=dt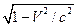 (15)-связывает собственное время dt0 с временем dt в К’.
(15)-связывает собственное время dt0 с временем dt в К’.
55.СТО. 4-х мерная формулировка-преобразование Лоренца и вращение в плоскости x, τ.
Математическое отступление. Формулы преобразования координат вектора при повороте в системе (здесь рисунок). Получим связь ax=>f1(ax;ay), ay=> f2(ax;ay), 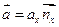 +ay
+ay y (1),
y (1), 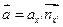 +ay’
+ay’ y’ (2)
y’ (2)
ax= x
x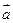 =
= x(ax’
x(ax’ x’+ay’
x’+ay’ y’)=ax’(
y’)=ax’( x
x x’)+ay’(
x’)+ay’( x
x y)
y)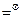 ax’cosj+ay’cos(
ax’cosj+ay’cos(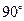 +j), ax=ax’cosj-ay’sinj(3)
+j), ax=ax’cosj-ay’sinj(3)
aα=Rαβaβ’ (4), Rαβ=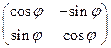 (5), a’x
(5), a’x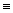 ax’ aα=
ax’ aα=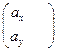 , a’α=
, a’α=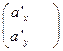 , ax=Rxxa’x+Rxya’y. Конец матем. отступления.
, ax=Rxxa’x+Rxya’y. Конец матем. отступления.
Введем формально четвертую координату. τ=ict (6). Будем считать, что формулы преобразования типа (3) и (4) справедливы и для координатной плоскости τx(здесь рисунок).
tgj=i(V/c) (7). Формулы преобразования (3) и (4) в точности совпадают с преобразованиями Лоренца (II).
cosj=1/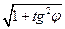 =1/
=1/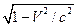 (8), sinj=cosjtgj, sinj=(iV/c)/
(8), sinj=cosjtgj, sinj=(iV/c)/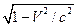 (9), (8) и (9) подставим в (3): x=(x’-τ’iV/c)/
(9), (8) и (9) подставим в (3): x=(x’-τ’iV/c)/ 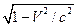 =(1/
=(1/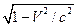 )(x’-ict’iV/c)=(x’+Vt’)/
)(x’-ict’iV/c)=(x’+Vt’)/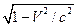 (I). Проверим вторую формулу τ=(x’iV/c+τ’)/
(I). Проверим вторую формулу τ=(x’iV/c+τ’)/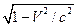 , ict=(x’iV/c+ict’)/
, ict=(x’iV/c+ict’)/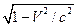 . t=(t’+x’V/c2)/
. t=(t’+x’V/c2)/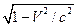 . Таким образом поварот системы координатной плоскости xτ на угол j, дает для x, y, z и t формулу Лоренца.
. Таким образом поварот системы координатной плоскости xτ на угол j, дает для x, y, z и t формулу Лоренца.
 2014-02-02
2014-02-02 1952
1952
