Множества. Примерный набор операций может быть следующим: Найти конкретную запись в наборе однотипных записей (инженера Сидорова)

Элементы теории множеств

Достоинства и недостатки

Ограничения целостности

Манипулирование данными

Примерный набор операций может быть следующим:

• Найти конкретную запись в наборе однотипных записей (инженера Сидорова);
• Перейти от предка к первому потомку по некоторой связи (к первому сотруднику отдела 310);
• Перейти к следующему потомку в некоторой связи (от Сидорова к Иванову);
• Перейти от потомка к предку по некоторой связи (найти отдел Сидорова);
• Создать новую запись;
• Уничтожить запись;
• Модифицировать запись;
• Включить в связь;
• Исключить из связи;
• Переставить в другую связь и т.д.

В принципе их поддержание не требуется, но иногда требуют целостности по ссылкам (как в иерархической модели).

Сильные места ранних СУБД:

1. Развитые средства управления данными во внешней памяти на низком уровне;
2. Возможность построения вручную эффективных прикладных систем;
3. Возможность экономии памяти за счет разделения подобъектов (в сетевых системах).

Недостатки:

Слишком сложно пользоваться;

1. Фактически необходимы знания о физической организации;
2. Прикладные системы зависят от этой организации;
3. Их логика перегружена деталями организации доступа к БД.

Наиболее простая структура данных, используемая в математике, имеет место в случае, когда между отдельными изолированными данными отсутствуют какие-либо взаимосвязи. Совокупность таких данных представляет собой множество. Понятие множества является неопределяемым понятием. Множество не обладает внутренней структурой. Множество можно представить себе как совокупность элементов, обладающих некоторым общим свойством. Для того чтобы некоторую совокупность элементов можно было назвать множеством, необходимо, чтобы выполнялись следующие условия:

1. Должно существовать правило, позволяющее определить, принадлежит ли указанный элемент данной совокупности.
2. Должно существовать правило, позволяющее отличать элементы друг от друга. (Это, в частности, означает, что множество не может содержать двух одинаковых элементов).

Множества обычно обозначаются заглавными латинскими буквами. Если элемент x принадлежит множеству A, то это обозначается: .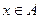

Если каждый элемент множества B является также и элементом множества A, то говорят, что множество B является подмножеством множества A: .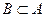

Подмножество B множества A называется собственным подмножеством, если .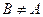

Используя понятие множества можно построить более сложные и содержательные объекты.