Определим статический момент полукруга

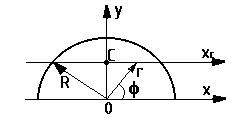
y_c =?

x_c = 0 (в силу симметрии)

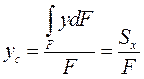
S_x =?

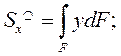
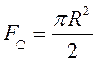
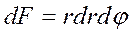
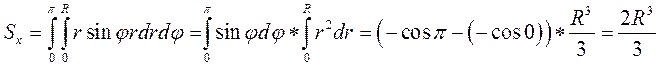
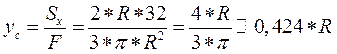
Осевыми (экваториальными) моментами инерции сечения называется интегралы вида:

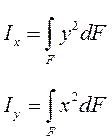
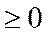
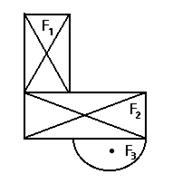
Если сечение площадью F можно представить в виде суммы нескольких замкнутых областей, то статический момент можно представить:

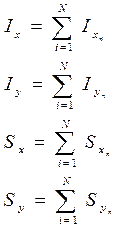
Полярный момент инерции сечения относительно начала координат – это интеграл вида:

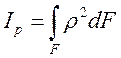
где r - полярный радиус

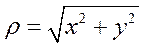
r 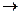(начальные координаты – (x; y)

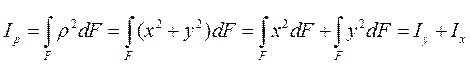
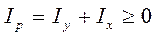
Центробежный момент инерции называется интеграл вида:

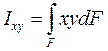
Размерность всех моментов инерции единица длины в 4 степени.

I_i [L⁴]

Главными осями инерции сечения называются две взаимно перпендикулярные оси, относительно которых

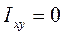
Если одна из взаимно перпендикулярных осей является осью симметрии сечения, то центробежный момент равен нулю I_xy=0, и следовательно обе оси являются главными.

Главными центральными инерциями сечения называются оси, проходящие через его центр тяжести.