Критерий наблюдаемости САУ

Рис. 2.34.

Очевидно, что эта система является ненаблюдаемой, так как не все переменные состояния 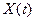могут быть восстановлены на основе выходного вектора 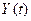(переменная состояния 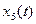является ненаблюдаемой переменной)

Пусть описание САУ представлено в терминах пространства состояния

САУ будет наблюдаемой тогда и только тогда, если матрица наблюдаемости имеет ранг 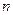.где 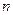- порядок системы (т. е. порядок вектора состояния ).

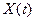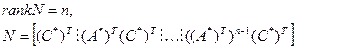(69)

Пример

Является ли система управляемой при ?

Матрица управляемости имеет вид:

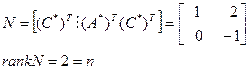
Следовательно, система является наблюдаемая.

Очевидно, что управляемость и наблюдаемость систем являются необходимыми условиями для синтеза САУ.