Критерий управляемости САУ

Рис. 2.33.

Очевидно, что эта система является неуправляемой, так как управляющее воздействие 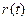влияет не на все переменные состояния (переменная состояния 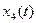не поддается управлению).

Существуют специальные правила (критерии), которые позволяют определить по структуре и параметрам объекта управляемость.

Пусть описание САУ представлено в терминах пространства состояния

САУ будет управляемой тогда и только тогда, если матрица управляемости имеет ранг 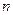.где 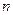- порядок системы (т. е. порядок вектора состояния ).

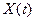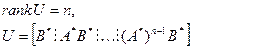, (67)

ранг матрицы – это наибольший порядок матрицы, имеющий ненулевой определитель.

Пример

Является ли система управляемой при ?

Матрица управляемости имеет вид:

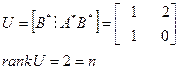
Следовательно система является управляемая.