2014-02-02
553
Простейший и классический процессы риска
Рассмотрим простейшую модель процесса риска в терминах следующей игры: в игре участвуют два игрока, в каждой партии первый игрок выигрывает единицу с вероятностью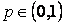 
и проигрывает единицу с вероятностью 
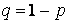. Суммарный начальный капитал обоих игроков равен а, начальный капитал первого игрока равен z; здесь a, z - целые числа, 
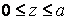. Таким образом, процесс описывается уравнением
где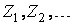 
последовательность независимых одинаково распределенных случайных величин с дискретным распределением,
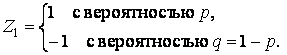
Игра заканчивается, когда обнуляется капитал одного из игроков (капитал первого игрока становится равным 0 или а), что трактуется, как разорение соответствующего игрока. Ясно, что при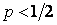 
игра невыгодна для первого игрока ввиду 
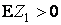, при 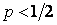- выгодна 
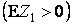, а при 
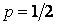является нейтральной, "справедливой": 
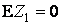. Обозначим 
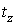момент разорения первого игрока: 
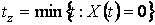(несобственная случайная величина), 
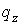вероятность разорения первого игрока при начальном капитале 
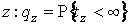. Отметим, что ввиду известной симметрии игры вероятность разорения 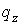второго игрока при начальном капитале первого, равном z, может быть вычислена формальной заменой а на 
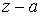и перестановкой р и q в выражении для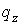
Если начальный капитал первого игрока равен 0 или а, то игра не проводится и соответствующие значения вероятностей разорения равны
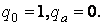
Если же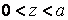 
, то после первой партии капитал первого игрока принимает значение 
с вероятностью р или значение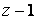 
с вероятностью q. Поэтому, по формуле полной вероятности,
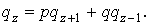
представляет собой разностное уравнение второго порядка с характеристическим уравнением
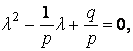
корни которого равны 1 и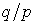 
, соответственно. Обозначим второй корень
