Задача о разорении. Вероятность разорения
Рис. 3.1. Распределение двух совокупностей 1 и 2 по признаку
Формула Байеса и оптимальные параметрические решающие правила могут быть использованы, если возможна достаточно точная аппроксимация функции плотности распределения данных.
Рассмотрим состояние страхового портфеля не только в конце более длинных периодов времени (чем год), но и в промежуточные моменты времени, вне зависимости от того, предъявляются ли страховой компании требования о выплате. В частности, обсудим вопрос: имеются ли у компании достаточные средства для того, чтобы оплатить потенциальные требования о выплате?
Сумма, которую компания имеет в момент времени t, называется активами на момент t. Ясно, что
| [Активы на момент t] = [Исходные активы] + [Взносы на момент t] – [Выплаты на момент t] | (3.1) |
Нашей целью будет определение вероятности разорения и ее зависимости от:
- начальных активов;
- надбавки безопасности.
Чтобы найти взаимосвязь предположим, что:
- требования о выплате, предъявляемые страхователями, оплачиваются немедленно;
- процентная ставка равна нулю;
- издержки страховщика во внимание не принимаются
Пусть:
N(t) - число требований о выплате, имевших место до момента t; t>0.
{N(t)} 0³t - случайный процесс, описывающий число требований о выплате.
Xi - размер i -й страховой выплаты.
S(t) - общий размер страховых выплат, имевших место до момента t, t>0.
{S(t)} 0³t - случайный процесс, описывающий общий размер выплат.
Для каждого t>0 имеем:
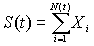 ,
,
U - начальные активы;
U(t) - активы страховщика в момент t.
Предположим, что страховые взносы поступают непрерывно и с фиксированной скоростью c. Тогда по (3.1) имеем
U(t)=U+ct-S(t)
Ясно, что {U(t)}t³0 - случайный процесс, называемый процессом изменения активов.
Когда активы падают до нуля, то говорят, что произошло разорениестраховщика.
Y(U) называется вероятностью окончательного разорения при данных начальных активах U:
Y (U)= Pr (u(t)<0, при некотором t, 0<t<¥)
Сложное пуассоновское распределение S ~ CP(l,F), если
1. Xj одинаково распределены с общей для них функцией распределения F(x)
2. Xj независимы от N
3. N ~ P(l)
В этом случае
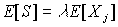
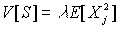
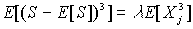
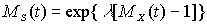
Введем дополнительные предположения:
а) случайные величины 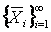 независимы и одинаково распределены (обозначим общую для всех Xi функцию распределения через F(x), плотность распределения через f(x));
независимы и одинаково распределены (обозначим общую для всех Xi функцию распределения через F(x), плотность распределения через f(x));
б) случайные величины 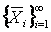 независимы от N(t) при всех t³0;
независимы от N(t) при всех t³0;
в) случайный процесс 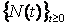 является пуассоновским с параметром l, т.е.
является пуассоновским с параметром l, т.е.
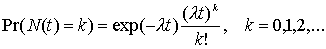
Тогда процесс {S(t)}t³ 0 является пуассоновским процессом.
Обозначим 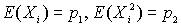 . Предположим, что страховые взносы, собранные страховщиком за единичный момент времени, превосходят ожидаемую величину страховых выплат за единицу времени
. Предположим, что страховые взносы, собранные страховщиком за единичный момент времени, превосходят ожидаемую величину страховых выплат за единицу времени
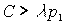
C можно записать в терминах относительной надбавки
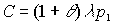
Предположим, что Mx(t) - производящая функция моментов для распределения страховых выплат.
 2014-02-02
2014-02-02 1180
1180







