Определение вероятности окончательного разорения в экспоненциальном случае

В общем случае Y (U) удовлетворяет уравнению

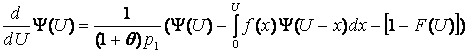
(3.5)

Это уравнение обычно решается с помощью численных методов. В случае экспоненциального распределения решением (3.5) является функция

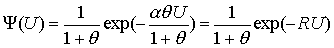
Приведенное решение позволяет провести исследование неравенства Лундберга в экспоненциальном случае (см. рис. 3.3).

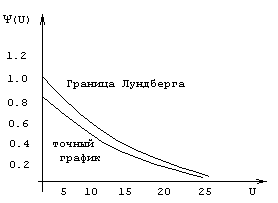
Рис. 3.3. Графики Y (U) и exp(-RU) в случае экспоненциальности страховых выплат со средним 1 и надбавкой безопасности q = 0,2.

На рисунке 3.4 показано, что вероятность разорения резко падает с увеличением надбавки безопасности.

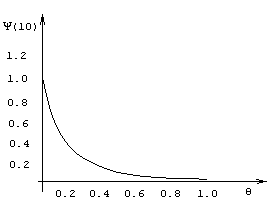
Рис 3.4. График зависимости Y(10) от q в случае, когда выплаты распределены экспоненциально со средним 1.