2014-02-02
2032
Моментом импульса материальной точки, вращающейся относительно неподвижной оси OO′, называется величина L, равная произведению импульса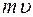 
этой точки на расстояние r от этой точки до оси вращения: 
.
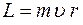Момент импульса является векторной величиной. Вектор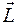 
направлен по оси вращения в соответствии с правилом правого винта.
При вращении твердого тела относительно неподвижной оси отдельные его точки, находящиеся на различном расстоянии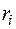 
от оси вращения, имеют различные скорости 
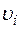. Поэтому, чтобы найти момент импульса твердого тела относительно некоторой оси вращения, необходимо разбить это тело на элементарные объемы так, чтобы каждый элементарный объем можно было бы рассматривать как материальную точку массой 
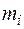, находящуюся на расстоянии 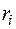от оси вращения, движущауюся со скоростью .
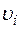Тогда момент импульса твердого тела L равен суммемоментов импульсавсех n материальных точек массами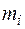 
, на которые разбито это тело:
.
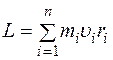Так как для твердого тела угловая скорость вращения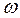 
всех материальных точек, на которые разбито это тело, одинакова, то, используя формулу 
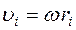, получим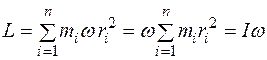 
|
|
|
или в векторной форме: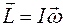 
.
Продифференцировав это уравнение по времени, получим:
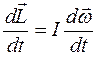, откуда 
.
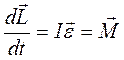То есть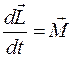 
.
Это выражение – еще одна форма уравнения динамики вращательного движения твердого тела: скорость изменения момента импульса твердого тела относительно оси вращения равна векторной сумме моментов всех действующих на это тело сил относительно той же оси вращения.
В замкнутой системе векторная сумма моментов внешних сил равна нулю. Тогда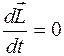 
и, следовательно, 
.
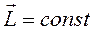Таким образом, момент импульса замкнутой системы сохраняется, что является законом сохранения момента импульса.
