Аналогично моменту силы определяется момент импульса 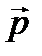 материальной точки относительно полюса О. Если на рис. 28 мы заменим вектор силы
материальной точки относительно полюса О. Если на рис. 28 мы заменим вектор силы 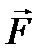 на вектор импульса
на вектор импульса 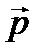 , то вектор
, то вектор 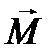 покажет направление вектора момента импульса. Момент импульса обозначается буквой L.
покажет направление вектора момента импульса. Момент импульса обозначается буквой L.
Момент импульса материальной точки относительно точки вращения О. Моментом импульса (L) материальной точки относительно точки О называется векторная физическая величина, равная векторному произведению радиус-вектора 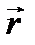 , проведенного из точки О в место нахождения материальной точки, на вектор ее импульса
, проведенного из точки О в место нахождения материальной точки, на вектор ее импульса 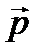 :
:
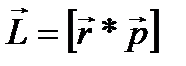 . (82)
. (82)
Модуль момента импульса материальной точки L = r*p*sin(α), где α – угол между векторами 
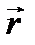 и
и 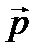 .
.
Размерность момента импульса – кг*м2/с.
Если материальная точка движется по окружности радиусом r, то модуль момента импульса относительно центра окружности равен
L = mvr, (83)
так как угол α между векторами 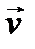 и
и 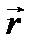 равен 900.
равен 900.
Перейдем в формуле (83) от линейной скорости к угловой согласно (24). Тогда получим:
L = mvr = mr2*ω = Jω, (84)
где J – момент инерции точки относительно центра окружности.
|
|
|
Моментом импульса материальной точки относительно оси, проходящей через эту точку, называется проекция момента импульса эту ось. По аналогии с формулой (81) можно написать:
Lz = Pп * d, (85)
где d – кратчайшее расстояние между осью и линией, вдоль которой направлен вектор 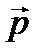 .
.
Иллюстрацией может служить рис. 29, на котором вектор 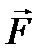 меняется на вектор
меняется на вектор 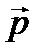 , а вектор
, а вектор 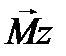 – на вектор
– на вектор 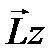 .
.
 2015-02-14
2015-02-14 1969
1969
