Сила, действующая на колеблющуюся материальную точку массой 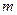
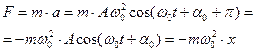 , (1.8.5)
, (1.8.5)
пропорциональна смещению  и направлена в сторону, противоположную смещению, т. е. к положению равновесия. Она называется квазиупругой силой, которая является консервативной. Поэтому при гармонических колебаниях нет перехода энергии механического движения в другие виды энергии – кинетическая энергия
и направлена в сторону, противоположную смещению, т. е. к положению равновесия. Она называется квазиупругой силой, которая является консервативной. Поэтому при гармонических колебаниях нет перехода энергии механического движения в другие виды энергии – кинетическая энергия  переходит в потенциальную
переходит в потенциальную 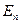 и обратно. Полная энергия системы остается постоянной.
и обратно. Полная энергия системы остается постоянной.
Кинетическая, потенциальная и полная энергии материальной точки, совершающей прямолинейные гармонические колебания, равны
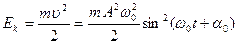 ; (1.8.6)
; (1.8.6)
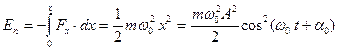 ; (1.8.7)
; (1.8.7)
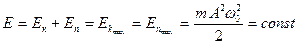 . (1.8.8)
. (1.8.8)
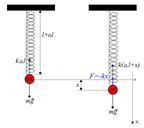 Рис.5.2 Рис.5.2 | 8.4. Гармонический осциллятор Гармоническим осциллятором называется система, закон движения которой описывается уравнением вида (1.8.4). Примерами гармонического осциллятора являются пружинный, физический и математический маятники. Пружинный маятник (рис.5.2) - груз массой 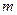 , подвешенный на абсолютно упругой пружине и совершающий колебания под действием квазиупругой силы: , подвешенный на абсолютно упругой пружине и совершающий колебания под действием квазиупругой силы:  ( (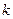 - жесткость пружины). - жесткость пружины). |
Закон движения маятника имеет вид:
|
|
|
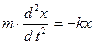 или
или 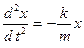 . (1.8.9)
. (1.8.9)
Сравнивая это уравнение с законом движения гармонического осциллятора (1.8.4), можно сделать вывод, что пружинный маятник совершает гармонические колебания по закону 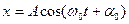 с циклической частотой и периодом равными
с циклической частотой и периодом равными
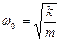 и
и 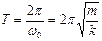 . (1.8.10)
. (1.8.10)
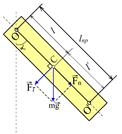 Рис.5.3 Рис.5.3 | Физический маятник (рис.5.3) - твердое тело, совершающее колебания под действием силы тяжести вокруг горизонтальной оси 0, не проходящей через его центр масс 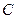 . При отклонении маятника на угол . При отклонении маятника на угол 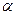 от положения равновесия составляющая силы тяжести от положения равновесия составляющая силы тяжести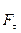 создает момент возвращающей силы, который при малых углах отклонения равен создает момент возвращающей силы, который при малых углах отклонения равен 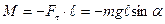 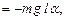 (1.8.11) (1.8.11) |
где 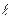 - длина физического маятника.
- длина физического маятника.
Подставив выражение (1.5.11) в основной закон динамики вращательного движения 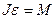 , получим:
, получим: 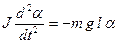 или
или 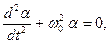 (1.8.12)
(1.8.12)
где 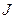 – момент инерции маятника относительно оси вращения.
– момент инерции маятника относительно оси вращения.
Это уравнение по виду совпадает с законом движения гармонического осциллятора. Следовательно, физический маятник совершает гармонические колебания с параметрами:
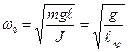 ;
; 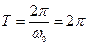
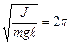
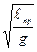 , (1.8.13)
, (1.8.13)
где длина 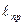 называется приведенной длиной физического маятника
называется приведенной длиной физического маятника 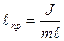 (1.8.14)
(1.8.14)
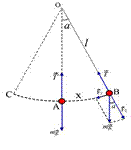 Рис.5.4 Рис.5.4 | Математический маятник (рис.5.4) - материальная точка массой 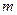 , подвешенная на невесомой и нерастяжимой нити длиной , подвешенная на невесомой и нерастяжимой нити длиной 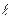 и колеблющаяся под действием силы тяжести без трения. Математический маятник можно рассматривать как частный случай физического маятника. Поэтому если в формулу (1.8.13) подставить момент инерции и колеблющаяся под действием силы тяжести без трения. Математический маятник можно рассматривать как частный случай физического маятника. Поэтому если в формулу (1.8.13) подставить момент инерции 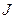 материальной точки относительно оси, проходящей через точку материальной точки относительно оси, проходящей через точку  ( (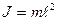 ), то получим формулу для периода колебаний математического маятника ), то получим формулу для периода колебаний математического маятника 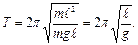 (1.8.15) (1.8.15) |
Из сопоставления формул (1.8.13) и (1.8.15) получается, что данный физический маятник будет иметь такой же период, что и математический маятник длиной  . Поэтому приведенная длина физического маятника – это длина такого математического маятник, период колебаний которого совпадает с периодом колебаний данного физического маятника.
. Поэтому приведенная длина физического маятника – это длина такого математического маятник, период колебаний которого совпадает с периодом колебаний данного физического маятника.
|
|
|
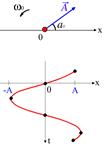 Рис.5.5 Рис.5.5 |
8.5. Представление гармонических колебаний с помощью вращающегося вектора амплитуды
Гармонические колебания, описываемые уравнением 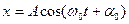 , можно представить с помощью вращающегося вектора амплитуды. Из точки 0, взятой на оси
, можно представить с помощью вращающегося вектора амплитуды. Из точки 0, взятой на оси  , под углом
, под углом 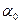 , равным начальной фазе колебания, отложим вектор длиной
, равным начальной фазе колебания, отложим вектор длиной 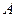 , равной амплитуде колебания (рис.5.5). Если привести этот вектор во вращение против движения часовой стрелки с угловой скоростью
, равной амплитуде колебания (рис.5.5). Если привести этот вектор во вращение против движения часовой стрелки с угловой скоростью 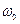 , то проекция его конца будет перемещаться по оси
, то проекция его конца будет перемещаться по оси  в пределах от
в пределах от 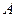 до
до 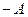 , причем координата проекции будет со временем изменяться по закону гармонического колебания. Схема, полученная таким способом, называется векторной диаграммой. Она широко используется при сложении колебаний, когда система одновременно участвует в нескольких колебательных процессах.
, причем координата проекции будет со временем изменяться по закону гармонического колебания. Схема, полученная таким способом, называется векторной диаграммой. Она широко используется при сложении колебаний, когда система одновременно участвует в нескольких колебательных процессах.
 2014-02-02
2014-02-02 8298
8298
