Перевод единичных критериев в относительные измерения

Переход от физических единиц измерения к относительным осуществляется с помощью функций перевода u_j (k_j). Отличительными особенностями функций перевода являют­ся:

– значения функций изменяются в интервале от нуля до единицы;

– имеется рабочий интервал аргумента от 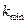до 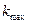, вне которого функция принимает постоянные значения. Нижняя и верхняя границы измерения аргумента определяют требования к объекту по рассматриваемому критерию.

Таким образом, для задания функции перевода необходимо задать ее вид и параметры, среди которых обязательными являются нижняя и верхняя границы.

Несмотря на многообразие функций перевода, можно привести несколько типовых функций, которые отражают боль­шинство случаев, встречающихся в практике решения многокритериальных задач.

Монотонные функции перевода. Рассмотрим сначала возрастающие монотонные функции перевода. Эти функции используются для перехода к относительным единицам из­мерения по критериям, при увеличении которых предпочтение объектов возрастает.

Линейная функция перевода определяется в соответ­ствии с выражением:

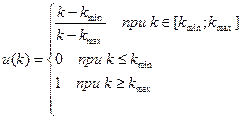
Линейная функция используется для перехода к относительным величинам, когда приращение полезности критерия не зависит от его значений, т.е. если увеличить аргумент на Δk, то приращение полезности Δu(k) будет одинаковым при разных k.

Показательная выпуклая вверх функция перевода определяется в соответствии с выражением:

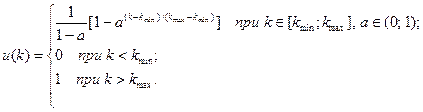
Данная функция используется в тех случаях, когда весьма существенны значения критерия, близкие к нижней границе, и критерий не влияет на полезность объектов при дальнейшем его увеличении до верхней границы.

Монотонные убывающие функции перевода u′(k) вычисля­ются на основе возрастающих функций в соответствии с выражением

u ′(k) = 1 - u (k).

Виды убывающих функций перевода те же, что и возраста­ющих.