Таблица 2.2
Матрица рангов
| Объекты | Зар. Плата | Удаленность | Перспективы |
| Вариант 1 | 5,5 | ||
| Вариант 2 | |||
| Вариант 3 | 4,5 | 5,5 | |
| Вариант 4 | |||
| Вариант 5 | 1,5 | ||
| Вариант 7 | 1,5 | ||
| Вариант 8 | 4,5 |
Этап 2. Упорядочение критериев по их важности. Обозначим ранги критериев через 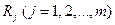 . Пусть в примере ранги критериев равны
. Пусть в примере ранги критериев равны 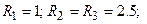 .
.
Этап 3. Вычисление проекций рангов 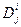 .
.
Проекции объединяют ранги объектов 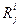 и ранги критериев
и ранги критериев 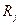 в число
в число 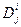 . Обычно используют:
. Обычно используют:
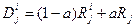 , где коэффициент
, где коэффициент 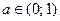 задается ЛПР. Коэффициент определяет в какой степени учитывать ранг критерия или ранги вариантов по каждому критерию.
задается ЛПР. Коэффициент определяет в какой степени учитывать ранг критерия или ранги вариантов по каждому критерию.
Чаще всего в качестве а используют ½, что соответствует учету рангов критериев и объектов в равной степени.
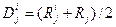 ,
,
В рассматриваемом примере используем 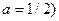 , тогда значения проекций равны:
, тогда значения проекций равны:
Проекции рангов
| Объекты | 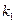 | 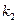 | 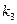 |
| Вариант 1 | 3,5 | 2,25 | |
| Вариант 2 | 1,75 | 3,25 | |
| Вариант 3 | 3,5 | ||
| Вариант 4 | 2,75 | 1,75 | |
| Вариант 5 | 1,25 | 4,75 | 2,75 |
| Вариант 7 | 1,25 | 4,25 | 4,75 |
| Вариант 8 | 2,5 | 3,5 | 2,25 |
Этап 4. Ранжирование вычисленных проекций, т.е. все элементы матрицы 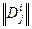 рассматриваются как одно множество, и по величине
рассматриваются как одно множество, и по величине 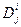 они упорядочиваются. Результаты ранжирования обозначим через
они упорядочиваются. Результаты ранжирования обозначим через 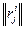 .
.
Ниже в таблице приведены результаты ранжирования для числового примера. Следует подчеркнуть, что процедура ранжирования проекций решает проблему агрегирования критериев.
Ранжирование проекций
| Объекты | 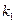 | 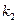 | 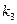 |  |
| Вариант 1 | 6,5 | 37,5 | ||
| Вариант 2 | 3,5 | 32,5 | ||
| Вариант 3 | ||||
| Вариант 4 | 9,5 | 3,5 | ||
| Вариант 5 | 1,5 | 20,5 | 9,5 | 31,5 |
| Вариант 7 | 1,5 | 20,5 | ||
| Вариант 8 | 6,5 | 28,5 |
Этап 5. Упорядочение вариантов (модификация 1 ORESTE)
Для рассмотренного примера  приведены в последней колонке таблицы рангов проекций. Соответственно порядок предпочтения объектов следующий:
приведены в последней колонке таблицы рангов проекций. Соответственно порядок предпочтения объектов следующий: 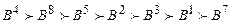 .
.
Необходимо отметить, что данные результаты упорядочения следует рассматривать как предварительное решение задачи. Если ЛПР удовлетворено полученным результатом, то процедура завершается, в противном случае переходим к следующему этапу.
Этап 6. Расчет коэффициентов предпочтения.
Предпочтение объекта i над объектом l (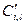 ) оценивается следующим образом:
) оценивается следующим образом:
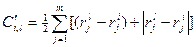 .
.
При вычислении 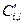 суммируются только положительные разности
суммируются только положительные разности 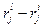 , тем самым суммируются разности рангов только по тем критериям, для которых
, тем самым суммируются разности рангов только по тем критериям, для которых 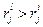 .
.
Максимально возможная разность 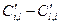 равна
равна 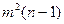 .Чтобы коэффициент предпочтения (Ci,l) изменялся в интервале [0;1], коэффициент
.Чтобы коэффициент предпочтения (Ci,l) изменялся в интервале [0;1], коэффициент 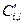 нормируют:
нормируют:
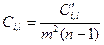 .
.
Для рассматриваемого числового примера значения коэффициенты предпочтения равны:
| Объекты | 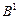 | 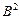 | 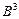 | 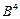 | 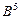 | 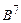 | 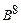 |
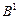 | 0,056 | 0,139 | 0,056 | 0,259 | 0,296 | 0,139 | |
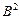 | 0,148 | 0,287 | 0,111 | 0,315 | 0,444 | 0,194 | |
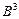 | 0,167 | 0,222 | 0,111 | 0,12 | 0,157 | 0,056 | |
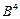 | 0,306 | 0,269 | 0,333 | 0,315 | 0,491 | 0,139 | |
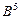 | 0,37 | 0,333 | 0,204 | 0,176 | 0,204 | 0,12 | |
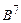 | 0,231 | 0,287 | 0,065 | 0,176 | 0,028 | 0,12 | |
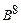 | 0,306 | 0,269 | 0,194 | 0,056 | 0,176 | 0,352 |
Этап 7. Установление отношений предпочтений (модификация 2 ORESTE)
Чтобы лучше понять правила установления отношений между объектами, представим данные о Ci,l и Cl,i в виде точки на плоскости, как показано на рис. 2.8.
Чем ближе точка к оси абсцисс, тем больше разность 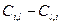 , т.е. с большим основанием можно говорить, что Вi предпочтительнее Вl. И наоборот, чем ближе точка к оси ординат, тем Вl предпочтительнее Вi.
, т.е. с большим основанием можно говорить, что Вi предпочтительнее Вl. И наоборот, чем ближе точка к оси ординат, тем Вl предпочтительнее Вi.
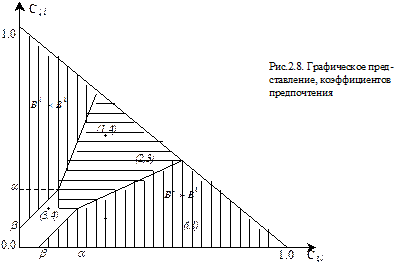 |
Если разность 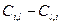 небольшая, и сами коэффициенты Ci,l и Cl,i малы, то между объектами Вl и Вi следует установить отношение безразличия. Чтобы сформулировать правила установления отношений между объектами, введем следующие пороги:
небольшая, и сами коэффициенты Ci,l и Cl,i малы, то между объектами Вl и Вi следует установить отношение безразличия. Чтобы сформулировать правила установления отношений между объектами, введем следующие пороги:
a и b (для определения отношения безразличия);
g > 0 (для определения отношения предпочтения).
Между объектами Вi и Вl устанавливаются:
a) отношение безразличия (Вi ~ Вl), если |Ci,l - Cl,i|£b, Ci,l£a и Cl,i£a;
b) отношение предпочтения (Вi f Вl), если |Ci,l - Cl,i|>b и 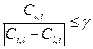 ;
;
c) Вi и Вl несравнимы (Вi N Вl), если между ними не установлены отношения предпочтения или безразличия.
Условие установления отношения предпочтения Вi f Вl можно переписать в следующем виде: 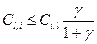 , а для Вl f Вi – в виде
, а для Вl f Вi – в виде 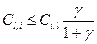 .
.
Чтобы задать бинарные отношения между объектами, достаточно определить пороги b и g, порог a вычисляется на основе b и g и равен b(1+g).
Порог g можно задавать любым, причем, чем меньше g, тем более жесткое условие для установления отношения предпочтения.
Что касается порога b, то он может принимать небольшое значение. Во-первых, чем меньше b, тем с большей уверенностью можно устанавливать отношение безразличия. Во-вторых, при больших b может оказаться, что Bi ~ Bl, в то время как один из них доминирует другой. Предельный случай, когда Bi может доминировать Bl:
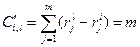 , а
, а 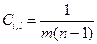 .
.
Значит, для b ограничение будет
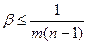 .
.
Если в исходном множестве нет доминируемых объектов, то ограничение для b) необязательно.
Отметим важное свойство отношения предпочтения. Показано, что отношение предпочтения транзитивно.
Рассмотрев вопросы установления бинарных отношений между объектами, вернемся к блок-схеме метода (рис.2.7). На седьмом этапе ЛПР должно задать пороги b и g, на основе которых строится матрица бинарных отношений.
Пусть в примере 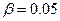 и
и 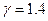 , тогда между объектами устанавливаются бинарные отношения, приведенные в таблице 2.6.
, тогда между объектами устанавливаются бинарные отношения, приведенные в таблице 2.6.
Варьируя порогами b и g, ЛПР может изменять связность графа предпочтения: при увеличении g увеличивается связность графа, причем все дуги, полученные при меньшем g,остаются, и к ним добавляются новые.
Если ЛПР не получило удовлетворяющее его решение, то целесообразно вернуться к первым этапам: ранжирование критериев (этап 2), выбор вида проекций (этап 3).
Матрица бинарных отношений
| Объекты | 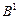 | 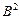 | 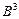 | 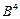 | 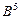 | 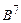 | 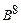 |
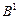 | ~ | < | N | < | N | N | < |
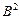 | > | ~ | N | < | N | N | N |
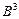 | N | N | ~ | < | N | > | < |
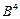 | > | > | > | ~ | > | > | > |
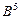 | N | N | N | < | ~ | > | N |
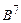 | N | N | < | < | < | ~ | < |
 | > | N | > | < | N | > | ~ |
В практических задачах число критериев может достигать нескольких десятков. Применять одну свертку ко всем критериям нельзя. Поэтому множество критериев необходимо структуризовать в виде дерева критериев, а затем проводить агрегирование критериев по дереву. Рассмотрим данный подход по его основным этапам:
– построения дерева критериев;
– перехода от различных физических единиц измерения единичных критериев к относительным величинам;
– задания операторов агрегирования критериев по дереву
– анализ результатов оценки и уточнение параметров (функций перевода в относительные единицы, веса критериев, операторов агрегирования).
 2014-02-02
2014-02-02 819
819








