Доказательство. Последнее равенство и дает основание утверждать справедливость данной теоремы

Пусть 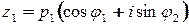, 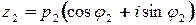. Тогда

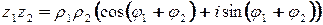. Последнее равенство и дает основание утверждать справедливость данной теоремы.

что и требовалось доказать.

Замечание. .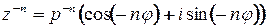

Корни - ой степени из единицы

Определение. Комплексное число 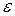называется корнем - ой степени из единицы, где 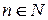, если .

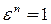Вычислим все корни - ой степени из единицы. Пусть 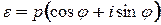. Зная, что 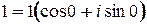, составим систему: 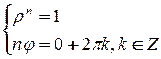. Тогда 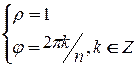и любой корень - ой степени из единицы будет иметь вид: .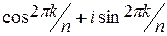

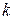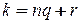Покажем, что существует ровно различных корней - ой степени из единицы. Для этого поделим на с остатком, получим , где 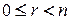. Следовательно, 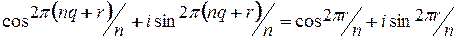. Поскольку 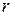может принимать только одно из значений 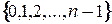, то и различных корней - ой степени из единицы также будет ровно штук, причем 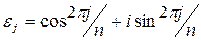, где .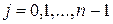

Теорема 3. Корни - ой степени из единицы образуют мультипликативную циклическую группу.