Пусть 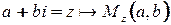 .
.
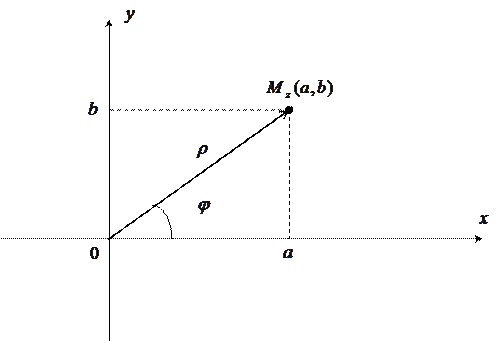
Каждому комплексному числу 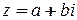 ставится в соответствие точка
ставится в соответствие точка 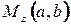 в прямоугольной системе координат.
в прямоугольной системе координат.
Если 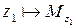 и
и 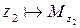 , то
, то 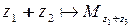 . При этом
. При этом 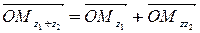 .
.
Тригонометрическая форма записи комплексного числа возникает из геометрической интерпретации. Так, каждой точке 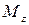 можно поставить в соответствие радиус-вектор
можно поставить в соответствие радиус-вектор 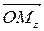 , который определяется длиной
, который определяется длиной 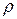 и направлением – углом
и направлением – углом 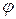 отклонения от положительного направления оси
отклонения от положительного направления оси  .
.
Замечание.  ,
, 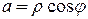 ,
, 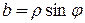 .
.
Таким образом 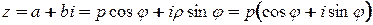 . Последняя запись и есть тригонометрическая форма записи комплексного числа.
. Последняя запись и есть тригонометрическая форма записи комплексного числа.
Предложение 2. Если 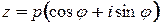 , то
, то 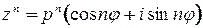 для каждого
для каждого 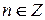 .
.
 2014-02-02
2014-02-02 787
787








