2014-02-02
572
Преобразование координат, матрица преобразований.
В некоторых случаях приходится одновременно рассматривать две системы координат на плоскости и решать следующию задачу: зная координаты точки в одной системе координат найти её координаты в другой системе. Формулы, выражающие координаты точки в одной системе, через её координаты в другой системе называются формулами преобразования координат. Рассмотрим две системы: xoy и x`o`y`
y y`
M(x;y)
0 x`
0 x
Система X`O`Y` может быть получена параллельным переносом осей Ох и Оу. Условимся называть координатны системы ХОY старыми, а Х`О`Y` - новыми. Предположим, что точка М на плоскости имеет старые координаты х и у и новые x` и y`.Из рисунка получим:
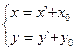(1)
Формулы (1) называются формулами параллельного переноса осей. Рассмотрим теперь в плоскости прямоугольную систему координат Х1ОХ2 с ортами е1 и е2
х
2
х`2 M x`1
e`2 e
e`2 e`1
φ
e1 x1
X1OX2 – старая система координат, X`1O`X`2 - новая система координат, с ортами e`1 и e`2
Начало координат старой и новой системы совпадают. Возьмем в плоскости произвольную точку М. Найдем связь между старыми и новыми координатами имеем:
ОМ = х1е1 + х2е2 и ОМ = x`1e`1 + x`1e`1+ x`2e`2, таким образом:
х1e1 + x2e2 = x`1e`1 + x`2e`2 (2)
Умножим обе части равенства (2) скалярно на е1, принимая е1е1=1 и е1е2=0
х1 = x`1(e1e`1)+x`2(e1e`2)
Умножая обе части (2) скалярно на е`2 получим:
х2 = x`1(e2e`1)+x`2(e2e`2) (3)
Введм обозначения:
α11 = e1e`1 = │e1││e`1│cos(e1;e`1) = cos(e1;e`1)
α12 = e1e`2 = cos(e1;e`2)
α21 = e2e`1 = cos(e2;e`1) (4)
α22 = e2e`2 = cos(e2;e`2)
Тогда равенства (2) и (3) можно записать в виде:
x1 = α11x`1 + α12x`2 (5)
x2 = α21x`1 + α22x`2
Формулы (5) называются формулами преобразования координат на плоскости, а матрица
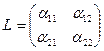
- матрицей преобразования.
Рассмотрим матрицы-столбцы: 
и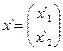 
. С помощью преобразования координат (5) в матричной форме запишем в виде: x = Lx`
Установим некоторые свойства матрицы L. Прежде всего найдем разложение векторов е1 и е2 по новому базису e`1 и e`2:
;
;
;
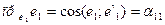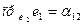, то
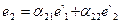(6)
Формулы (6) дают разложение векторов е1 и е2, по базису е`1 и e`2. Аналогично получим разложение e`1 и e`2 по базису e1 и e2:
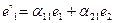
(7)
Так как е1е1=1 и е1е2=0, то примая во внимание (4) и (6) получим:
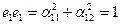
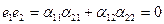(8)
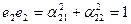
Аналогично: е`1е`1=1 и е`1е`2=0 получим из (4) и (7)
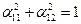
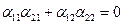(9)
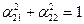
Матрица L обладает следующими свойствами:
а) сумма квадратов элементов строки (столбца) равна 1
б) сумма парных произведений элементов строки (столбца) на соответсвующие элементы другой строки (столбца) равна 0
Матрица обладающая этими свойствами называется ортогональной.
Рассмотрим транспонированную матрицу L:
, с учетом (8) имеем:
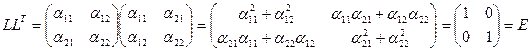
Таким образом матрица LT является обратной для матрицы L, тоесть
L-1=LT=
(10)
Пусть новая система координат получена из старой системы, поворотом осей на угол α. В этом случае:
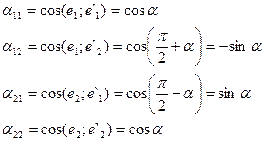
Следовательно формулы (5) принимают вид:
x1 = x`1cosα+ x`2sinα (11)
x2 = x`1sinα+ x`2cosα
Формулы (11) называются формулами поворота осей.
